Категориальный поиск трехмерных фигур испытуемыми с разным уровнем математической экспертизы

Дренёва Анна Александровна Московский государственный университет имени М.В. Ломоносова

Введение

Десятилетия исследований в области зрительного поиска обеспечили бога­тый материал, объясняющий механиз­мы того, как мы ищем и находим объ­екты в окружающем мире (Wolfe, 1998; Eckstein, 2011). Одной из характерных тенденций в области зрительного поиска является постепенный переход от более простых стимулов: отдельных точек, сим­волов, простейших форм к более слож­ным, семантически нагруженным стиму­лам, реалистичным фотоизображениям объектов (Zelinsky et al., 1997), рисункам (Henderson, Weeks, Hollingworth, 1999) и, наконец, полностью реалистичным сценам (Eckstein, Drescher, Shimozaki, 2006; Zelinsky, Schmidt, 2009).

Такой переход естественным образом связан с изменением типа поисковой за­дачи. Если в ранних исследованиях цель задавалась предельно конкретно и чаще всего представлялась в виде конкретно­го объекта, то впоследствии целевой сти­мул стал задаваться в виде текста с его названием – вербальной инструкции. Такая задача получила название категориаль­ного поиска, при котором целевой объ­ект задается понятием, категорией. Дан­ный тип задачи специфичен тем, что цель имеет не конкретные физические черты, она может принимать вид любого из представителей заданной категории и может появиться в любом виде и под любым углом. Такая задача, безусловно, является гораздо более сложной и при этом экологичной – в реальной жизни мы редко ищем конкретную урну, чтобы выбросить обертку, или конкретную ко­фейню, чтобы быстро перекусить в не­знакомом месте (Zelinsky et al., 2013).

Разумеется, ввиду повышенной слож­ности категориального поиска с вер­бальной инструкцией, по сравнению с поиском конкретного образа цели, эф­фективность выполнения задачи категориального поиска ниже (Wolfe et al., 2004; Vickery, King, Jiang, 2005). Однако снижен­ная эффективность поиска не означает, что он неуправляем. По данным иссле­дования Zelinsky и коллег, категориаль­но заданные цели фиксировались с пер­вой же саккады чаще, чем можно было бы ожидать при случайном поиске (Yang, Zelinsky, 2009), а степень «управляемости» поиска возрастала с увеличением количе­ства вербальной информации о целевом стимуле (Schmidt, Zelinsky, 2009).

В серии наших исследований мы ис­пользуем объекты, репрезентирующие математические понятия. В предыдущих экспериментах (Кричевец и др., 2017; Дренёва и др., 2019) мы изучали процесс выполнения задачи на категориальный поиск на материале простых геометри­ческих фигур (квадрат, круг, треуголь­ник, крест), двумерных геометрических фигур (четырехугольники разных видов) и трехмерных фигур (пирамиды и призмы). Результаты проведенных ис­следований подтвердили естественные гипотезы: концептуальная сложность фи­гур, наряду с факторами схожести ди­страктора и ориентацией в простран­стве, оказывают влияние на скорость и эффективность поиска. Такая зависи­мость может иметь место, только если испытуемый анализирует стимулы еще до перевода объектов интереса в зону фовеа. Такой анализ естественно назвать экстрафовеальным (термин экстрафовеа в современной литературе употребля­ется для объединения парафовеальной и периферической зон зрительного поля). К эктрафовеальному анализу мы отнесем процессы преаттентивной па­раллельной обработки зрительного поля и скрытого внимания, которые будут рас­смотрены далее.

Естественной тенденцией в области зрительного поиска является изменение фиксируемых параметров. Если в нача­ле изучения механизмов поиска визу­альных объектов наиболее популярными параметрами фиксации выступали вре­мя моторной реакции и точность ответа (Wolfe et al., 2004), то с середины 90-х го­дов прошлого века стали использоваться параметры движений глаз (Findlay, 1997; Williams et al., 1997; Zelinsky, Sheinberg, 1997), в частности, в ситуациях категориального поиска, такой показатель, как направление первой саккады (Chen, Zelinsky, 2006; Schmidt, Zelinsky, 2011; Zelinsky et al., 2013). В наших исследо­ваниях (Кричевец и др., 2017; Дренёва и др., 2019) мы использовали сходный, но более информативный параметр – ко­личество посещенных секторов до до­стижения сектора с целевым стимулом. Данный показатель позволяет выявить не только наличие ранней параллельной обработки всех стимулов, предваряющей программирование первой саккады, но также уровень эффективности экстра­фовеального анализа при программиро­вании последующих саккад. Если учиты­вать, насколько выражено отличие этого показателя от соответствующего случай­ному просмотру всех представленных объектов.

Безусловно, процесс зрительного пои­ска тесно связан с механизмами внима­ния, обеспечивающими более высокую эффективность идентификации объ­ектов и их конкретных характеристик (Treisman, Gelade, 1980; Zhang et al., 2008). Многие модели внимания постулируют, что процессы, функционирующие«сверху вниз» (top-down), с самого начала оказы­вают значительное влияние на процесс программирования саккад (Rosenholtz, Huang, Ehinger, 2012). В контексте ог­раниченных ресурсов внимания преаттентивный анализ объектов, то есть осуществляемый еще до привлечения внимания, может проводиться по все­му полю одновременно, после чего вни­мание переносится на один конкретный объект для более тщательного изучения. Выделяется также особый вид внима­ния – скрытое внимание (Posner, 1980; Deubel, 2008), перемещающееся по зри­тельному полю без сопутствующих дви­жений глаз. В данном исследовании спе­циальные серии, в которых инструкцией вводился запрет на движения глаз, позво­лили сфокусироваться исключительно на экстрафовеальном анализе стимулов с помощью скрытого внимания.

В нашем исследовании для изучения возможностей экстрафовеального ана­лиза в качестве стимульного материа­ла использовались достаточно сложные трехмерные фигуры – пирамиды, экстра­фовеальное распознавание которых пред­ставляет для испытуемых трудную задачу (Дренёва и др., 2019), в отличии от отно­сительно простых задач, описанных в дру­гой работе (Кричевец и др., 2017). Мы рас­считывали, что в этой сложной ситуации наилучшим образом выявится главный предмет нашего интереса – межинидиви­дуальные различия, которые могут прояв­ляться в различных перцептивных и ког­нитивных стратегиях решения задачи. Такие различия могут быть вызваны лич­ностными особенностями, разным уров­нем мотивации (Gandini, Lemaire, Dufau, 2008; Frömer et al., 2015), а также различ­ным уровнем экспертизы в области, реле­вантной предъявляемым стимулам. В на­шем исследовании мы контролировали только последний фактор.

Исследования движений глаз «экспер­тов» (математиков, физиков, программи­стов) показали, что они способны более быстро и точно находить релевантные объекты (Gegenfurtner, Lehtinen, Säljö, 2011; Чумаченко, Шварц, 2016) и быст­рее выделять ключевые стимулы из шума (Goodwin, 1994). Кроме того, существу­ют данные о том, что математическое образование обеспечивает более эффек­тивное выделение структур в паттернах (Radford, 2010) и использование неоче­видных эвристик при решении задач на ориентировку в координатной плоско­сти (Krichevets, Shvarts, Chumachenko, 2014). Опираясь на эти работы, мы пред­полагали, что наличие математического образования скажется на результате ре­шения задачи категориального поиска сложных геометрических фигур.

Основной целью данного исследова­ния выступило изучение эффективности решения задачи категориального зри­тельного поиска на материале сложных трехмерных фигур, в частности, изучение возможностей экстрафовеального анализа стимулов в обычных пробах, раз­решающих движения глаз, и специаль­ных, в которых вводился запрет на дви­жения глаз. Кроме того, в исследовании ставилась цель изучения роли математи­ческой экспертизы в контексте эффективности поиска сложных геометриче­ских фигур.

Проведение исследования

Выборка. Выборка включала две под­группы: «эксперты» (математики, физики, программисты, имевшие или получавшие соответствующее образование) и «нович­ки» (психологи). В первой группе было 15 человек (из них 7 женщин), во второй – 17 человек (из них 16 женщин). Возраст варьировал от 18 до 25 лет. Все участники имели нормальное или скорректирован­ное до нормального зрение.

Аппаратно-программные характе­ристики. Движения глаз записывались с помощью установки SMIRED с часто­той регистрации положения взгляда 120 Гц. Запись проводилась с исполь­зованием программы iViewX, стимуль­ный материал предъявлялся в програм­ме ExperimentCenter 3.3. Экран монитора имел размеры 19 дюймов по диагонали. Испытуемые находились на расстоянии 60 см от экрана, голова не фиксирова­лась. В начале эксперимента проводилась двенадцатиточечная калибровка с вали­дизацией, по результатам которой испы­туемые допускались к участию в эксперименте. Критерием допуска выступало достижение калибровочной точности не более 0,5 градуса.

Процедура. Испытуемым предъявля­лась следующая инструкция: «Вашей за­дачей является нахождение стереометри­ческих фигур (четырех- и пятиугольных пирамид), указанных в инструкции. Про­читав инструкцию, переведите взгляд на фиксационный крест. После этого поя­вится слайд с четырьмя фигурами, из ко­торых Вы должны будете выбрать нуж­ную. Как только Вы ее найдете, нажмите на пробел и назовите букву сектора, в котором она находилась. Постарайтесь выполнять задания как можно быстрее и правильнее». Перед каждым предъяв­лением слайда со стимулами на экране появлялась текстовая инструкция в виде названия целевой фигуры. Перед второй и последней сериями, в которых вводил­ся запрет на движения глаз из центра экрана, предъявлялась инструкция: «Вни­мание! Постарайтесь выполнять задания, не переводя взгляд из центра экрана».

Стимулы представляли собой слайды с трех-, четырех-, пяти- и шестиугольной пирамидами, равноудаленными от цен­тра на расстояние 4–6 угловых градусов (рисунок 1). Задачей испытуемого было, в зависимости от инструкции, находить 4-х или 5-ти угольную пирамиду как мож­но скорее и точнее. Варьировались следующие факторы: тип цели (4-х или 5-ти угольная пирамида), разрешение/запрет на движения глаз, расположение в одном из четырех секторов. Последний фактор варьировался квазирандомизированным образом.

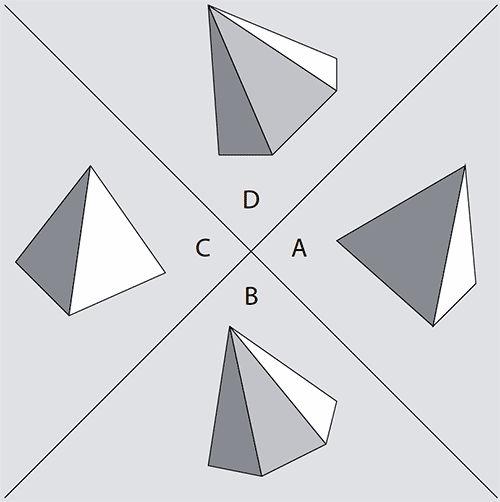
Рис. 1. Образец стимульного слайда

В эксперименте было 9 серий по 16 проб. При этом во 2-й и 9-й сериях ин­струкцией вводился запрет на движения глаз, и угол взора к плоскости основа­ния фигур был 35 градусов, а не 25, как в остальных сериях, для оценки качества переноса навыка распознавания пирамид на новые изображения фигур. Первая се­рия являлась тренировочной и не учиты­валась при анализе результатов.

Всего было предъявлено 144 слайда: в первой части 80, во второй – 64, с неболь­шим перерывом между частями (от пяти до пятнадцати минут). В каждой серии из 16 стимулов следовало 8 проб подряд с четырехугольной пирамидой и 8 – с пя­тиугольной. Тип цели чередовался.

Обработка данных. Обработка дан­ных в этом эксперименте включала в себя анализ не только стандартных по­казателей – времени и правильности от­вета. Как мы писали во введении, вместо частоты направления первой саккады на цель (Chen, Zelinsky, 2006; Schmidt, Zelinsky, 2011; Zelinsky et al., 2013), мы ис­пользуем в наших исследованиях длину последовательности посещений зон со стимулами до посещения целевой зоны. Этот показатель рассчитывался следую­щим образом.

С помощью программы Begaze 3.3 экран со стимулами делился на 5 зон интереса: 4 сектора со стимулами и центральная зона. Далее учитывалось количество посещенных зон в последовательности фиксаций до достижения сектора с целевой фигурой – порядко­вый номер целевой зоны. Повторные по­сещения зон не учитывались. Поскольку количество посещенных зон при случай­ном поиске сектора с целевой фигурой равно (1+2+3+4)/4=2,5, именно с этим числом сравнивались средние индивиду­альные показатели (в принципе, возмо­жен случай, когда, посетив три зоны без целевого стимула, испытуемый методом исключения определяет правильный от­вет, однако такие случаи не встретились в более чем четырех тысячах проб). В се­рии наших исследований экстрафовеаль­ного восприятия мы обозначаем этот по­казатель FirstT.

Статистическая обработка данных осуществлялась с помощью программы IBM SPSS Statistics version 21.

Результаты

В результате эксперимента были по­лучены 4162 пробы по 29 испытуемым. Пробы еще троих участников недоступ­ны для анализа по техническим при­чинам. Сравнительный межгрупповой анализ количества правильных ответов показал следующие результаты: «экспер­ты» в среднем дали 74,2% правильных ответов, «новички» – 70,1%. Что свидетельствует о значительной сложности категориального поиска при таком сти­мульном материале. Важно, что значи­мых различий между группами обнару­жено не было (таблица 1).

Табл. 1. Количество правильных ответов в группах математиков и психологов

Математики («эксперты»)		Психологи («новички»)
Инициалы испытуемого	Количество правильных ответов (%)	Инициалы испытуемого	Количество правильных ответов (%)
V	58,9	T	50
A1	65,3	A4	50,7
M1	68,5	A5	54,9
A2	68,7	M3	55,2
A3	69,2	I	56,6
Y	69,9	M4	62,5
N	70,6	D2	69,7
E1	72,1	V	74,8
E2	72,9	E3	76,1
D1	74,1	M5	77,8
S	90,2	K2	78
K1	91	A6	81,1
M2	93,1	A7	82,6
K3		82,6
A8		84
D3		85
Среднее арифметическое	74,2	Среднее арифметическое	70,1
Медиана	70,6	Медиана	75,45

Отсутствие значимых различий меж­ду двумя группами может указывать на то, что данная задача требует использо­вания навыка, несвязанного напрямую с образовательным профилем. По дан­ным постэкспериментального интервью было выявлено, что участники из группы психологов, давшие наибольшее число правильных ответов (81% и выше), в дей­ствительности имели достаточно обшир­ный опыт работы со схематизированны­ми изображениями трехмерных фигур, например, посещали художественную школу, дополнительно занимались сте­реометрией, изготавливали макеты трех­мерных фигур, изучали основы дизайна и так далее.

Поскольку различий между «экспер­тами» и «новичками» во всех видах обра­ботки не обнаруживается, мы приводим далее только результаты по объединен­ной выборке. При рассмотрении трени­ровочных серий от третьей до восьмой одновыборочный Т-критерий сравнения по всем испытуемым среднего индиви­дуального значения FirstT со значением 2,5, соответствующим случайному пои­ску, дает t(28) = 4,9, p = 0,00004 (крите­рий знаковых рангов дает p = 0,0001). При расчете средних индивидуальных значений мы учитывали здесь только пробы, заканчивающиеся правильным ответом. Правомерность такой фильтра­ции не бесспорна. Можно возразить, что правильные ответы даются на более про­стые задания. Однако, если включать все пробы, независимо от правильности, ре­зультат только усиливается (t(28) = 5,3). Таким образом, экстрафовеальный ана­лиз стимулов, несомненно, имеет место в среднем по выборке.

Однако характеристика «в среднем» затушевывает тот очевидный факт, что некоторые испытуемые демонстриру­ют впечатляющие индивидуальные ре­зультаты. Одновыборочный T-критерий сравнения индивидуальных значений показателя FirstT в соответствующих про­бах дает у семи испытуемых p< 0,001 – значимость, выдерживающую поправ­ку Бонферрони для 29 сравнений. Мы отдаем себе отчет, что использование T-критерия для дискретного и асимме­тричного распределения дает уязвимый результат, но вместе с корректным опи­санным выше подтверждением резуль­тата в среднем эти значимости можно считать достаточно убедительным сви­детельством того, что некоторые испы­туемые используют экстрафовеальный анализ при программировании саккад. Доказать, что некоторые другие испыту­емые такой анализ не используют, разумеется, невозможно, но приведенная на рисунке 2 гистограмма распределения средних показателей по испытуемым го­ворит о том, что это, вероятно, так. Мода распределения находится вблизи точки 2,5, в то время как наиболее способные испытуемые определяют бросающуюся в глаза асимметрию распределения.

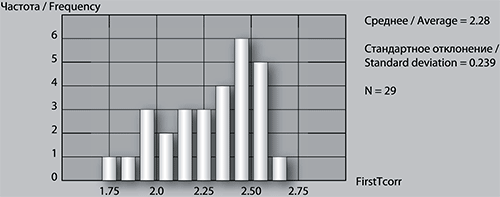
Рис. 2. Гистограмма распределения средних показателей FirstT по испытуемым

Интересно также проанализировать динамику показателя FirstT в процессе тренировки. Отрицательная корреляция между номером пробы и значением FirstT для данного испытуемого является ин­дикатором все более эффективного ис­пользования экстрафовеального анализа и способности находить целевую фигуру при просматривании все меньшего чи­сла секторов. Такая корреляция была об­наружена всего у 3 испытуемых (у всех трех значимости меньше 0,02, но не вы­держивают поправку Бонферрони). Зна­чимое ухудшение параметра, то есть по­ложительная корреляция номера пробы с FirstT, наблюдалась у двух участников (p = 0,004 и p = 0,0015 – последняя вы­держивает поправку Бонферрони для 29 сравнений). Хотя в среднем коэффици­ент корреляции близок к нулю, все же то, что мы имеем дело с усреднением разно­направленных тенденций, подтверждает­ся следующим расчетом. Рассмотрим, как зависит динамика FirstT от демонстриру­емого данным испытуемым среднего по­казателя FirstT. График рассеяния приве­ден на рисунке 3.

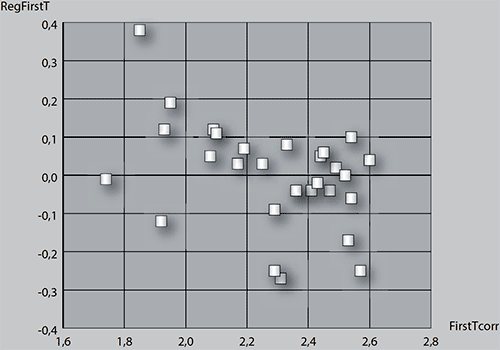
Рис. 3. Взаимосвязь динамики показателя FirstT и среднего FirstT по испытуемым

Коэффициент корреляции Спирме­на равен -0,36 (p = 0,055). При этом пир­соновский коэффициент дает лучший результат. Мы видим, что разнонаправ­ленная динамика согласуется со сред­ним уровнем показателя. Например, ис­пытуемый, показавший второй результат среднего по FirstT, демонстрирует мак­симальное ухудшение этого показателя в процессе тренировки (для него следовало бы сказать «антитренировки»). Бо­лее того, обе значимости его результатов выдерживают поправку Бонферрони на множественные сравнения.

Перейдем теперь к рассмотрению ре­зультатов контрольных серий 2 и 9, в ко­торых инструкцией вводился запрет на движения глаз из центра экрана. Про­бы из этих серий, в которых были выявлены движения глаз вне центральной зоны, исключались из анализа. По итогам контрольных серий было обнаружено, что различия средних между группами математиков и психологов минималь­ны (0,56 и 0,57 во второй серии и 0,68 и 0,69 в девятой соответственно). При объединении групп среднее индивидуаль­ных частот правильных ответов значи­тельно выше в 9-й серии, по сравнению со 2-й – 0,68 и 0,56 соответственно и раз­личия значимы – t(28)= 2,71, p = 0,011 (p = 0.027 в непараметрическом вари­анте). При сравнении частот с частотой угадывания 0,25 отличия выглядят до­стоверными (во второй и девятой сери­ях t(28) равно 7,5 и 16,4 соответственно). Поскольку треугольная пирамида похо­жа на четырехугольную, а пятиугольная – на шестиугольную, то есть выбор из по­хожих пар представляется более лег­кой задачей, чем выбор из четырех фи­гур, мы также сравнили значения частот с частотой 0,5, соответствующей случайному угадыванию целевой фигуры при предшествующем правильном определе­нии пары схожих с целевой фигур. Таким образом, с помощью одновыборочного Т-критерия мы измерили здесь чистое экстрафовеальное распознавание целе­вой фигуры «с запасом».

По второй серии среднее значение ча­стот, как уже говорилось, составило 0,56, t(28)=1,49, p=0,15, по девятой серии – 0,68, t(29)=6,99, p<0,000001 (непараме­трический аналог дает p = 0,0002). Этот поразительный результат говорит о том, что при запрете движений глаз задача рас­познавания цели решается испытуемыми в среднем достаточно успешно. При этом частота меньше 0,5 в 9-й серии наблюда­ется лишь у двух испытуемых, а два луч­ших участника выполнили все шестнад­цать проб без движений глаз и допустили суммарно всего одну ошибку. При этом корреляции между процентами правиль­ных ответов во второй и девятой сериях, с одной стороны, и средним индивиду­альным значением FirstT, с другой, малы и равны – 0,085 и 0,11 соответственно. Та­ким образом, можно говорить о том, что, во-первых, научение экстрафовеально­му анализу фигур произошло, во-вторых, при соответствующей инструкции экстра­фовеальный анализ достаточно эффекти­вен и, в-третьих, в процессе планирования саккад экстрафовеальный анализ, возможность которого продемонстрировала 9-я серия, не используется в полной мере.

Обсуждение

Результаты данного исследования по­зволяют сделать вывод о том, что кате­гориальный поиск трехмерных пирамид оказался достаточно сложным для всех испытуемых, что отразилось в количест­ве посещенных зон близком к случайно­му, а также в невысокой эффективности экстрафовеального анализа в пробах со свободной инструкцией. При этом ана­лиз проб, в которых нельзя было пере­водить взгляд за пределы центральной зоны, выявил, что достаточно точный экстрафовеальный анализ, тем не менее, вполне возможен для большинства испы­туемых, хотя и не используется ими, ког­да запрета на движения глаз нет.

Другой важной находкой данного ис­следования является обнаружение мо­дификации поведения конкретных ис­пытуемых в процессе решения задачи категориального поиска, причем, у каж­дого участника это изменение носило индивидуальный характер. Отмечались не только специфические стратегии, с использованием или игнорированием данных экстрафовеального анализа при решении задачи, но также различные виды трансформации этих стратегий в процессе эксперимента.

Например, одни испытуемые демон­стрировали успешное обучение кате­гориальному поиску, что выражалось в сокращении числа посещенных зон и, следовательно, в улучшении показате­ля эффективности экстрафовеального анализа. Другие испытуемые, изначаль­но более успешно различавшие стиму­лы и имевшие более высокий показатель эффективности экстрафовеального ана­лиза, могли с течением эксперимента демонстрировать его ухудшение, за кото­рым, возможно, стояла выработка единой стратегии для всех задач, ввиду возмож­ной энергозатратности экстрафовеаль­ного анализа. Можно предполагать, что на эффективность поиска оказывали влияние такие факторы, как индивидуальные особенности участников, их перцептив­ные и когнитивные стратегии, а также ситуационная мотивация. Такие резуль­таты согласуются с другими работами по данной теме (Gandini, Lemaire, Dufau, 2008; Fromer et al., 2015). Таким образом, можно говорить об межиндивидуальных различиях в стратегиях зрительного по­иска у каждого из испытуемых, а также о специфическом их изменении в про­цессе эксперимента.

Кроме того, по результатам экспе­римента было выявлено, что распозна­вание сложных геометрических фигур и уровень эффективности экстрафове­ального анализа не имеют прямой свя­зи с образовательным профилем участ­ников. Определенное влияние при этом может иметь наличие соответствующего опыта работы с трехмерными объектами, знания и навыки в области изобразитель­ного искусства и архитектуры.

Дополнительно было обнаружено определенное научение экстрафовеаль­ному анализу у большинства испыту­емых, которое выражалось в большем числе правильных ответов во второй контрольной серии, по сравнению с пер­вой. В этом контексте интересно то, что в данном эксперименте средний FirstT (2,26) по всем испытуемым значимо от­личался от случайных – 2,5, а также от результатов нашего предыдущего иссле­дования (Дренёва и др., 2019), в кото­ром средние значения FirstT в сериях с третьей по восьмую варьировали по ис­пытуемым от 2,21 до 2,78 (там же). Един­ственным отличием между этим экспериментом и предшествующим было наличие во второй серии запрета на дви­жения глаз, что могло дать испытуемым соответствующую установку на более ак­тивное использование экстрафовеально­го анализа в процессе поиска.

Поскольку в данном эксперимен­те использовались довольно сложные трехмерные фигуры, мы можем с уве­ренностью говорить о вовлеченности категоризации в процесс решения пои­сковой задачи. Другими словами, мы изучали обработку не только низкоуровне­вых перцептивных признаков объектов, но также анализ характеристик гораздо более высокого уровня, обеспечиваемо­го мыслительными операциями категоризации и навыком работы с соответствующими сложными стимулами. Влияние механизмов top-down на процесс вос­приятия было показано и в других ра­ботах (Rosenholtz, Huang, Ehinger, 2012). Применительно к нашему исследованию, похожие результаты были получены Yang и Zelinsky, которые показали, что задача поиска категориально заданного объекта среди изображений произвольных быто­вых предметов может быть решена экстрафовеально (Yang, Zelinsky, 2009).

Заключение

Результаты данного исследования про­демонстрировали, что при решении зада­чи категориального поиска трехмерных геометрических фигур одновременно за­действованы процессы экстрафовеального и фовеального анализов стимулов. Данные процессы сложным образом взаимодействуют между собой, при этом дина­мика этого взаимодействия может опреде­ляться индивидуальными особенностями субъектов, спецификой задачи и инструк­ции и механизмами нижнего уровня, обеспечивающими быструю автомати­ческую обработку признаков. Значимым результатом стало обнаружение и иссле­дование межиндивидуальных различий, которые проявились не только в опреде­ленной степени использования экстра­фовеального анализа, но также в степе­ни изменения стратегии решения задачи и уровне научения категориальному пои­ску в процессе прохождения эксперимен­та. Изучение роли скрытого внимания в специальных сериях, в которых инструк­цией вводился запрет на движения глаз, дали материал для глубокой дальнейшей проработки феномена экстрафовеально­го анализа, поскольку, даже если он наблюдается не во всех ситуациях и не у всех испытуемых при свободной инструк­ции, он, тем не менее, все равно возможен. Перспектива дальнейших исследований затрагивает условия, поощряющие его использование, например, уже примененное нами ограничение перемещений взгля­да, ограничение времени решения или предъявления стимулов. Исследование глазодвигательного поведения испытуе­мых в таких условиях поможет более пол­но изучить процессы экстрафовеального анализа зрительного поля и особенности его взаимодействия с другими системами перцепции, внимания и мышления.

Информация о грантах и благодарностях

Литература

Дренёва А.А. и др. Экстрафовеальный анализ категориально заданных трехмерных фигур // Сибирский психологический журнал. – 2019. – № 72. – С. 68–92. 10.17223/17267080/72/4

Кричевец А.Н. и др. Возможности экстрафовеального восприятия геометрических фигур // Вопросы психологии. – 2017. – №. 6. – С. 117–128.

Чумаченко Д.В., Шварц А.Ю. Проблема трансформации перцептивных процессов в ходе обучения: анализ исследований, выполненных методом записи движений глаз, с позиций деятельностного подхода [Электронный ресурс] // Психологические исследования : электронный научный журнал. – 2016. – Т. 9. – №. 49. – С. 12–12 : [сайт]. URL: http://psystudy.ru/num/2016v9n49/1329-chumachenko49

Chen X., & Zelinsky G.J. (2006). Real-world visual search is dominated by top-down guidance. Vision research, 46(24), 4118–4133. doi: 10.1016/j. visres.2006.08.008

Deubel H. (2008). The time course of presaccadic attention shifts. Psychological research, 72(6), 630. doi: 10.1007/s00426-008-0165-3

Eckstein M.P. (2011). Visual search: A retrospective. Journal of vision, 11(5), 14–14. doi: 10.1167/11.5.14

Eckstein M.P., Drescher B.A., & Shimozaki S.S. (2006). Attentional cues in real scenes, saccadic targeting, and Bayesian priors. Psychological science, 17(11), 973–980. doi: 10.1111/j.1467-9280.2006.01815.x

Findlay J.M. (1997). Saccade target selection during visual search. Vision research, 37(5), 617–631. doi: 10.1016/S0042-6989(96)00218-0

Frömer R. et al. (2015). Are individual differences in reading speed related to extrafoveal visual acuity and crowding? PloS one, 10(3), / doi: 10.1371/ journal.pone.0121986

Gandini D., Lemaire P., & Dufau S. (2008). Older and younger adults’ strategies in approximate quantification. Acta psychological, 129(1), 175–189. doi: 10.1016/j.actpsy.2008.05.009

Gegenfurtner A., Lehtinen E., & Säljö R. (2011). Expertise differences in the comprehension of visualizations: A meta-analysis of eye-tracking research in professional domains. Educational Psychology Review, 23(4), 523–552. doi: 10.1007/s10648-011-9174-7

Goodwin C. (1994). Professional vision. American anthropologist, 96(3), 606–633. doi: 10.1525/aa.1994.96.3.02a00100

Henderson J.M., Weeks Jr P.A., & Hollingworth A. (1999). The effects of semantic consistency on eye movements during complex scene viewing. Journal of experimental psychology: Human perception and performance, 25(1), 210. doi: 10.1037/0096-1523.25.1.210

Krichevets A.N., Shvarts A.Y., & Chumachenko D.V. (2014). Perceptual action of novices and experts in operating visual representations of a mathematical concept. [Psikhologiya. Zhurnal Vysshey shkoly ekonomiki], 11(3), 55–78.

Posner M.I. (1980). Orienting of attention. Quarterly journal of experimental psychology, 32(1), 3–25. doi: 10.1080/00335558008248231

Radford L. (2010). The eye as a theoretician: Seeing structures in generalizing activities. For the learning of mathematics, 30(2), 2–7. doi: 10.2307/20749442

Rosenholtz R., Huang J., & Ehinger K.A. (2012). Rethinking the role of top-down attention in vision: Effects attributable to a lossy representation in peripheral vision. Frontiers in psychology, 3(13). doi: 10.3389/fpsyg.2012.00013

Schmidt J., & Zelinsky G.J. (2009). Search guidance is proportional to the categorical specificity of a target cue. The Quarterly Journal of Experimental Psychology, 62(10), 1904–1914. doi: 10.1080/17470210902853530

Schmidt J., Zelinsky G.J. (2011). Visual search guidance is best after a short delay. Vision Research, 51(6), 535–545. doi: 10.1016/j.visres.2011.01.013

Treisman A. M., & Gelade G. (1980). A feature-integration theory of attention. Cognitive psychology, 12(1), 97–136. doi: 10.1016/0010-0285(80)90005-5

Vickery T.J., King L.W., & Jiang Y. (2005). Setting up the target template in visual search. Journal of Vision, 5(1), 8–8. doi: 10.1167/5.1.8

Williams D.E. et al. (1997). Patterns of eye movements during parallel and serial visual search tasks. Canadian Journal of Experimental Psychology/ Revue canadienne de psychologieexpérimentale, 51(2), 151. doi: 10.1037/1196-1961.51.2.151

Wolfe J.M. et al. (2004). How fast can you change your mind? The speed of top-down guidance in visual search. Vision research, 44(12), 1411–1426. doi: 10.1016/j.visres.2003.11.024

Wolfe J.M. (1998). What can 1 million trials tell us about visual search? Psychological Science, 9(1), 33–39. doi: 10.1111/1467-9280.00006

Yang H., & Zelinsky G.J. (2009). Visual search is guided to categorically-defined targets. Vision research, 49(16), 2095–2103. doi: 10.1016/j. visres.2009.05.017

Zelinsky G.J. et al. (1997). Eye movements reveal the spatiotemporal dynamics of visual search. Psychological science, 8(6), 448–453. doi: 10.1111/j.1467- 9280.1997.tb00459.x

Zelinsky G.J. et al. (2013). Modelling eye movements in a categorical search task. Philosophical Transactions of the Royal Society B: Biological Sciences, 368(1628). doi:10.1098/rstb.2013.0058

Zelinsky G.J., & Schmidt J. (2009). An effect of referential scene constraint on search implies scene segmentation. Visual Cognition, 17(6–7), 1004–1028. doi: 10.1080/13506280902764315

Zelinsky G.J., & Sheinberg D.L. (1997). Eye movements during parallel–serial visual search. Journal of Experimental Psychology: Human Perception and Performance, 23(1), 244. 10.1037/0096-1523.23.1.244

Zhang L. et al. (2008). SUN: A Bayesian framework for saliency using natural statistics. Journal of vision, 8(7), 32–32. doi: 10.1167/8.7.32