Фрактально-голографический конструкт и теория поля К. Левина

Богатых Борис Александрович Институт атомной энергетики Национального исследовательского ядерного университета МИФИ (ИАТЭ НИЯУ МИФИ)

Введение

Как известно, к 20-м годам прошлого века зародилось философское течение – неопозитивизм (эмпиризм). Он про­возгласил язык физики единственно на­учным, на который должны быть переведены, в том числе в целом, все суждения о психологических фактах (Современ­ная западная философия, 2000). Однако К. Левина это не устраивало. Он смотрел на физику несколько иначе. Его инте­ресовали, прежде всего, не те или иные операциональные процедуры и не пер­спективы сведения неопределенных пси­хологических понятий к физической тер­минологии, а интеллектуальные приемы (Левин, 2001). Именно они, по его мне­нию, могут обеспечить триумфальное об­новление новой психологии. В одной из первых своих работ он предпринял важное методологическое исследование раз­личий и приемов древнегреческой науки – физики Аристотеля, и физики нового времени – физики Галилея (Левин, 2001, С. 54–84). Основным выводом данной ра­боты К. Левина стало то, что симптомом прогресса в любой науке будет процесс перехода от так называемых вещных по­нятий, т.е. понятий, соответствующих реальным вещам в природе, к «реляци­онным» понятиям. Последние подразу­мевают, в том числе и в психологии, не столько однозначно определенные вещи, сколько изменчивые отношения, т.е. возможность разночтений и отличных одно от других истолкований.

К. Левин был первым, кто на этой ме­тодологической основе в прошлом веке систематически использовал коэволюци­онные связи жизненного пространства человека и его непсихологического мира при анализе сопряженного развития пси­хики. Он утверждал, что психологическая теория должна быть многомерной, т.е. должна рассматриваться в рамках теории поля. Именно теория поля позволяет ос­мыслить психологическую систему как систему многих взаимодействующих переменных, а не как совокупность их пар.

Заметим, что выработанное осново­положниками квантовой физики поня­тие о динамическом поле стало центром гештальтистских объяснений. Этот мо­мент как раз и роднил К. Левина с основателями гештальтпсихологии – М. Вер­тгеймером, В. Келером и К. Коффкой, занимавшихся проблемой перцептивных структур, т.е. категории образа. Понятие «динамическое поле» репрезентирует тот факт, что каждый пункт взаимодействует с другими, а, в свою очередь, изменение напряжения в одном из пунктов поро­ждает тенденцию к устранению данного напряжения и, в конечном итоге, ведет к восстановлению динамического напря­жения. К. Левин, в отличие от гештальти­стов, взял за основу анализа категорию мотива. Он считал, что мотивами являют­ся те или иные объекты, представляющие собой различные районы «жизненного пространства» в их отношении к тому человеку, который испытывает в них по­требность либо квазипотребность, т.е. намерение. Введением понятия «психо­логическое поле» К. Левин пытался опи­сать не физическую, а психологическую реальность, в которой живет человек. Ученый пытался этим отразить совокуп­ность событий, имеющих для человека смысл, обусловливающих его поведение в значимых жизненных ситуациях.

Иными словами, по К. Левину, моти­вами становятся сами предметы жизнен­ного пространства (окружающей среды) в силу потребностного отношения к ним человека (Левин, 2001). Причем, сама ди­намическая система означает не столько поле сознания, но и, прежде всего, поле поведения, которое в определенной мере детерминировано. Здесь динамическая система, отражающая собой поле пове­дения, представляет собой функцию пси­хического поля как системы, находящей­ся под напряжением, которое возникает при нарушении равновесия между чело­веком и средой. Следовательно, мотива­ции придавался собственно психологи­ческий статус. Таким образом, К. Левин сменил представление о замкнутости энергии мотива в пределах организма на представление о системе «организм – среда», что привело к рассмотрению че­ловека и окружающей его среды (физи­ческой, социальной и т.д.) в виде взаи­мосвязанного динамического целого. Как следствие, мотивационное напряже­ние стало выступать уже не как биологи­чески предопределенное, а как созданное конкретным человеком (в виде намере­ния, т.е. квазипотребности) либо другими людьми, взаимодействующими с данным человеком. Но, при этом возникла про­блема. Какое отношение имеет физика к психологическим феноменам? Можно ли интерпретировать психологические феномены, используя понятие динами­ческого поля? Ведь сама концепция ди­намического поля взята из физики. Сам К. Левин осмысливал данную проблему и пытался от физики перейти к геоме­трии, в частности, к топологии – науке, изучающей те или иные преобразования пространства (Levin, 1936).

К. Левин не застал создание ни прин­ципа голографии, ни фрактальной гео­метрии. Они были созданы уже после его смерти. На наш взгляд, опираясь на коэ­волюционные репрезентации исследо­вания сопряженного развития психики человека, его жизненного пространства и непсихологического мира, на обра­щение к фрактально-голографическо­му конструкту позволит, в определенной мере, представить психологические фе­номены в более обобщенных формах. Этому, на наш взгляд, соответствует тот факт, что фрактально-голографический конструкт не в последнюю очередь обес­печивает гармоничное существование и сосуществование конкретных систем, а также циклические процессы их с сис­темами более высокого порядка.

Таким образом, учитывая, что созна­ние психически взаимодействует с фи­зической реальностью, целью настоящей статьи является поиск подходов к объ­яснению различных психических феноменов и природы сознания в рамках природы фрактально-голографического конструкта, с привлечением его наибо­лее адекватного физического и матема­тического инструментария. Применение математического инструментария фрак­тально-голографического конструкта для адекватного объяснения психологи­ческих феноменов будет ново и весьма актуально. Это, на наш взгляд, позволит в последующем в рамках современной постнеклассической парадигмы в определенной мере модифицировать пред­ставления теории поля К. Левина.

Природа фрактально-голографического конструкта

Фрактальная геометрия

Рассматривая фрактальную геоме­трию можно отметить, что процессы, от­ражающие фрактальное самоподобие, основаны, прежде всего, на принципе обратной связи, когда результат одной итерации является начальным значени­ем следующей итерации. Наряду с этим, фрактальная геометрия позволяет уста­навливать взаимозависимость между ге­ометриями в различных масштабах, а именно, понимать, как микроскопиче­ское поведение тех или иных систем свя­зано с тем, что можно наблюдать в ма­кроскопическом масштабе (Mandelbrot 1980; 1982). Многообразие фракталов при этом, содержащих множество вир­туальных наборов всех возможностей, отраженное через принцип самоподо­бия, описывается довольно простой ма­тематической формулой вида: Z_n+1 = Z²_n + C . Данная формула получила на­звание множества Мандельброта (ММ). В ней, как мы отметили выше, отражен процесс повторения процедуры неопре­деленное число раз (процесс итерации), фиксируя этим непрерывное изменение и самоизменение опосредованного опе­рацией непрерывного самоотнесения (самореферентности). Процессу итерации, отраженному в данной формуле, со­ответствуют как золотая пропорция (ЗП), выступающая прообразом рядов (чисел) Фибоначчи (РФ), так и разного вида ге­ометрические и алгебраические прогрес­сии. Широкие исследования в области фрактальной геометрии и синергетики выявили глубокую связь между этими на­учными направлениями (Шелепин, 2001). Так, например, математический язык фракталов точно и корректно описывает тонкую структуру странных (фракталь­ных) аттракторов.

Синтетические взаимоотношения динамичности и статистичности

Важный аспект фрактальной геоме­трии заключается в том, что она содер­жит в себе, в рамках диалектического принципа, эффекты синергии, т.е. «коо­перативные», синтетические взаимоотношения динамичности и статистично­сти (Богатых, 2006; 2012). Динамичность системы – это фундаментальное качест­во развития системы как целого, так как именно оно связано с однозначной пред­сказуемостью, детерминированностью развития тех или иных систем и процессов между точками выбора путей эво­люции (точки бифуркации). Статистич­ность (стохастичность, случайность, т.е. сами точки бифуркации) – фундамен­тальное качество системы, относится к уровню ее элементного строения, на ко­тором будут возникать различного рода мутации, кардинально преобразуя сис­тему. Важно отметить, что, когда система попадает в точку бифуркации, ее поведе­ние в ней зависит от предыдущей исто­рии системы, оно уникально для данной системы. Иными словами, в данной ре­альности, которой внутренне присуща динамичность и статистичность, просма­тривается синтез позитивных элементов детерминистической и вероятностной картин мира, отражая собой в этом спе­цифическом единстве противоположно­стей саморазвитие органического мира (Богатых, 2006; 2012).

Фрактальная размерность

Само понятие размерности фракталь­ного множества Б. Мандельброт пред­ложил применять с целью количествен­ного описания фрактальных множеств. В более общей форме Мандельброт предлагает следующее определение фрактала: «Фракталом называется мно­жество, размерность Хаусдорфа-Бези­ковича для которого строго больше его топологической размерности» (Мандельброт, 2002). Данное определение, в свою очередь, требует определений терминов: «размерность Хаусдорфа-Бе­зиковича», т.е. дробная (фрактальная) размерность (D), и «топологическая раз­мерность» (Dт), которая всегда равна це­лому числу. В обыденном понимании размерность геометрического множест­ва (фрактальный рост) представляет со­бой число измерений, с помощью кото­рых можно задать положение точки на геометрическом объекте. И все же смысл понятия «размерность» значительно шире, так как оно отражает более «тон­кие» топологические свойства объектов, совпадая при этом с числом независи­мых переменных, необходимых для опи­сания объекта только в частных случаях. Так, распространение данного представ­ления на множество Кантора даст уже дробную размерность: dCantor = 0.63. Размерность кривой Коха: dKokh = 1.261. Рассмотренные объекты, как и ряд дру­гих объектов: кривая Пеано, ковер Сер­пинского и т.д. демонстрируют фун­даментальное свойство фрактальных объектов, их самоподобие, являющееся общим для всех фракталов (Mandelbrot, 1982; Кроновер, 2000).

Голография

Как известно, голография представля­ет собой трехмерную, безлинзовую фо­тографию, и способна воспроизводить объемные реалистичные образы матери­альных объектов. Математические осно­вы голографической техники были раз­работаны Денисом Габором еще в конце 40-х годов ХХ-го века. Сами голограммы выражаются при этом в форме так назы­ваемых преобразований Фурье, в основе которых – любой самый сложный пат­терн может быть разложен на ряд регу­лярных волн. Обратное преобразование Фурье, как и ряд других сходных с ними преобразований, при наличии правил трансформации превращает гологра­фическую сферу в структурированную. Иными словами, переводит волновой паттерн снова в изображение. Здесь не в последнюю очередь срабатывает осо­бое свойство голограммы, а именно, тот факт, что каждая часть голограммы, отра­жающая целое, обусловлена частностями математического преобразования карти­ны или паттерна в язык волновых форм. Именно данные преобразования позво­лили Д. Габору перевести изображение объекта в интерференционное «пятно» на голографической пленке и изобрести способ обратного преобразования ин­терференционных паттернов в первона­чальное изображение.

Самоподобные структуры в голографии

Важнейшим физическим принципом, лежащим в основе голографии, являет­ся принцип Гюйгенса-Френеля. Суть его в том, что каждая точка фронта волны, ис­ходящей из какого-либо источника света (рис. 1, А), представляет собой центр вторичного возмущения. Этот центр, в свою очередь, вызывает элементарные сферические волны (рис. 1, В), а волно­вой фронт в более поздние моменты вре­мени становится огибающим эти волны (рис. 1, С). Если продолжить умозритель­но эту цепочку дальше, то получим, что каждый фронт второго порядка создает источники и фронты третьего, четверто­го порядка (рис. 2) и т.д. Видно, что при таком распространении волны получается своеобразная самоподобная структу­ра, где каждый «источник» n-го порядка подобен всем источникам «предыдущих» порядков, и каждый фрагмент волны по­добен всей волне.

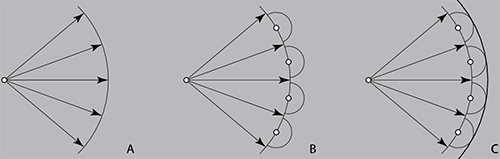
Рис. 1. Распространение волнового фронта. А. Фронт первичной волны. В. Вторичные источники элементарных волн. С. Огибающая вторич­ных источников, совпадающая с первоначальным фронтом.

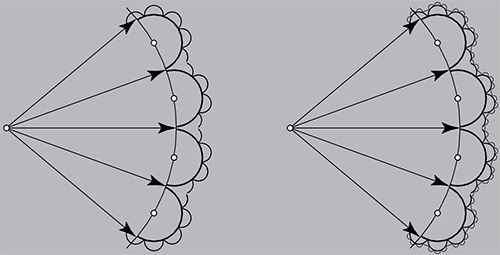
Рис. 2. Фронты третьего и четвертого порядков.

Иными словами, наличествует само­подобный конструкт – скейлинг или масштабная инвариантность. Аналогич­ное свойство масштабной инвариантно­сти сохраняет и голографическая пленка и, как следствие, любой фрагмент плен­ки способен восстановить весь исходный образ. Учитывая, что принцип Гюйгенса- Френеля в оптической голографии игра­ет основополагающую роль, можно пред­положить, что, моделируя, например, символьное рассеивание информации, можно также столкнуться с проявления­ми самоподобия.

Голограммы обладают также уникаль­ной способностью к хранению информации. Например, голографическая пленка может содержать более сотни изображе­ний на одной и той же поверхности. Та­ким образом, на каждую точку голограм­мы фактически проецируется сразу весь образ, обеспечивая многократно повто­ренную, избыточную информацию. Дан­ная колоссальная избыточность гологра­фической записи обеспечивает высокую помехоустойчивость и надежность хра­нения информации.

Фрактально-голографический конструкт

В целом фракталы являются близким структурным описанием голограммы, позволяя тем самым обозначать данное образование как фрактально-гологра­фический конструкт. При этом оба конструкта – фрактальность и голография – имеют дело с законами, уточняющими отношения между элементами или систе­мами, образующими организацию фрак­тально-голографического конструкта. Структура данной организации стано­вится более организованной при нара­стании большого количества степеней свободы, обеспечивая этим перекрыва­ние элементов, входящих в систему при максимально возможных отношениях элементов. Данная особенность позволя­ет осуществлять процесс перекрывания элементов данных конструктов – фрак­тальности и голографии, что обусловли­вает их взаимосодействие и постоянный переход идеального (фрактальность) в материальное образование (физика голограммы). Причем, данный переход осуществляется как в одну, так и в другую сторону, постоянно обогащая и обновляя элементы данных конструктов.

Немарковские процессы

Можно отметить, что качественное отличие работы мозга, осуществляюще­го мышление, от работы компьютера за­ключается в том, что в основе функци­онирования мозга лежит не заданный алгоритм, а стохастические немарков­ские процессы, которые описывают из­менение структур, обладающих памятью. Это, прежде всего, мозг как система, а так­же многие биологические, социальные и информационные системы, они стали наиболее адекватным инструментарием при описании процессов с памятью.

Рассматривая марковские процессы, следует отметить, что они обладают ло­кальностью во времени. Это, в принци­пе, позволяет определять вероятностную картину поведения системы в будущем, так как данная картина не меняется от добавочных сведений о событиях при t < t0. Таким образом, для марковских процессов вероятностная картина пове­дения системы в будущем определяется ее состоянием в момент времени t₀:

u_n+1 = ƒ(u_n). (1)

В немарковских же процессах важней­шей дополнительной характеристикой выступает негэнтропия как мера упоря­дочения структуры, мера ее сложности. Учитывая добавочные сведения о собы­тиях при t < t₀ , т.е. память о прошлом, не­марковские процессы по своей природе являются нелокальными во времени. Ве­роятностная картина для них в простей­шем случае будет иметь вид:

u_n+1 = u_n + u_n-1 (2)

Характерная величина un данного уравнения зависит не только от преды­дущего состояния, но также и от того, что было шаг назад, т.е. от событий при t < t₀. Ближняя память, отраженная в рекуррентном соотношении (2), является наиболее существенной для многих би­ологических явлений, она задает первое приближение в отклонении от марков­ского мира.

Именно теории немарковских про­цессов, описывающие изменение струк­тур обладающих памятью, а это, прежде всего, биологические, социальные и ин­формационные системы – стали наибо­лее адекватным инструментарием при описании процессов с памятью (Азро­янц и др., 1999; Шелепин, 2001). При этом именно ЗП, как и РФ, непосредст­венно следуют из условий равновесия в немарковской системе с ближней памя­тью (Богатых, 2012). Более того, как РФ, так и ЗП тесно связаны с немарковски­ми неравновесными распределениями и, следовательно, являются не только ха­рактеристиками и своего рода индикато­рами наличия немарковских процессов, но также служат признаками равновесия в таких системах (Шелепин, 2001).

В дополнение к этому предлагается выделять среди различных обобщений чисел Фибоначчи решение немарковско­го уравнения в виде:

u_n+1 = u_n + u_{n – Ѕ -1}, (3),

где каждый член равен сумме преды­дущего и отстоящего на определенную величину, а именно, Ѕ шагов (Шелепин, 2001). Причем, если Ѕ = 1, то оно будет соответствовать числам Фибоначчи, значениям же Ѕ = 2, 3, 4… – соответствуют ве­личины, носящие название Ѕ–чисел Фи­боначчи, способствующие обобщению понятия золотой пропорции. В этом слу­чае золотая Ѕ-пропорция будет являться положительным корнем уравнения золо­того Ѕ-сечения:

q^2Ѕ – q^Ѕ – 1 = 0. (4)

Вследствие этого, отношения со­седних Ѕ-чисел Фибоначчи совпадают в пределе с золотыми Ѕ-пропорциями аналогично обычному ряду Фибоначчи. Иными словами, золотые Ѕ-сечения являются числовыми инвариантами Ѕ-чи­сел Фибоначчи. В качестве примера, ин­варианты для первых четырех значений Ѕ соответственно равны: 1.618, 1.464, 1.380, 1.324. Следовательно, золотых сечений существует столько, сколько есть нату­ральных чисел k, т.е. целый ряд. Таким образом, золотая Ѕ-пропорция выражает более общий закон пропорционального отношения между целым и его частями, чем классическая золотая пропорция.

Способы достижения самоподобия в представлении символьной информации

Одним из основных источников са­моподобия фрактальных структур явля­ются итерации и рекурсивные функции, представляющие собой механизм обрат­ных связей. Он выполняет основной и всеобщий способ детерминации мно­гих явлений, состояний, процессов и т.д. Итерационные, как и рекурсивные, осо­бенности характерны для любых слож­ных самоорганизующихся, саморазвивающихся систем, обладающих при этом избыточной информацией. В данных системах можно увидеть организацию как идею и главные отношения, консти­туирующие и структурирующие систему, и собственно структуру как текущие вто­ростепенные связи, поддерживающие и сохраняющие организацию, меняющи­еся в целях и в рамках этого сохранения при появлении принципиально нового, эмерджентного. В качестве примеров в голографии может выступать ряд воз­можных вариантов создания избыточной информации для создания квазигологра­фической памяти в виде символьной ин­формации, а именно, последователь­ность Морса-Туэ, последовательность Фибоначчи, преобразование Прибрама, немарковские процессы (Шелепин, 2001; Шредер, 2005; Pribram, 1971).

Корпускулярно-волновой дуализм

Голографическое свойство фрактала, как и его самоподобие, выражающееся в наличии целого в каждой его части, по­зволяет привлекать его синергетичность при объяснении феноменов идеально­го: процессов мышления, чувствования, сознания. Данные психологические фе­номены (процессы мышления, чувство­вания, сознания) человек разворачивает в процессе своего существования само­подобным, фрактально-голографиче­ским способом спонтанно, естественным образом в соответствии с теми культурой, обычаями и нравами, в среде которых он сформировался как человек. Иными словами, человек реагирует на широкий спектр тех или иных событий при взаи­модействии с окружающей средой, как на ментальном, так и на биологическом уровне. Так, Д. Бом выражает точку зре­ния, согласно которой человек реагирует на те или иные события при взаимодей­ствии с окружающей средой, как на мен­тальном, так и на биологическом уровне. Он, в частности, отстаивает важный вы­вод, что смыслы присутствуют одновре­менно, как в психическом (сознание), так и в физическом (наша соматика) аспек­тах природы. Иными словами, сознание – это не единственный атрибут, реагиру­ющий на смыслы (Bohm, 1986, p. 123; Bohm, Hiley, 1994). В.В. Налимов, разви­вая эти представления, пишет: «Сознание человека породило изысканные геоме­трические представления, как для пони­мания Мира, так и для понимания само­го себя. И почему тогда не допустить, что сама природа, порождая многообразие форм – построений чисто геометриче­ских, – не опирается на геометрически задаваемую потенциальность» (Налимов, 2000, С. 142). Это вытекает из того фак­та, что сознание обладает такой же при­родой, как и все известные физические процессы, а именно, дуальностью волны/ частицы.

Как известно, природа корпускуляр­но-волнового дуализма материальных объектов микромира разрешилась Н. Бо­ром в рамках его знаменитого «принци­па дополнительности». Это указывает нам на то, что для адекватного описания суб­атомных явлений необходимо руковод­ствоваться не каким-то одним представ­лением о квантовом процессе (волновом или дискретном, корпускулярном), а дву­мя или более одновременно. Данный корпускулярно-волновой дуализм, выявленный для микрообъектов, Луи де Бройль распространил на все виды ма­терии (макро- и мегамиры), получив при этом простую зависимость, в которой между собой связаны как ее корпускуляр­ные (энергия, масса, скорость передви­жения), так и волновые свойства. Соглас­но де Бройлю, с любым материальным объектом связана волна, частота кото­рой прямо пропорциональна (а длина – обратно пропорциональна) произведе­нию массы частицы на ее скорость:

λ = b/mv, (5)

где b – постоянная Планка; m – масса, а v – скорость частицы (Де Бройль, 1965).

Для нас же важно, что данный корпу­скулярно-волновой дуализм применим и к макротелам и, соответственно, тре­бует применимости других основопо­лагающих принципов. Так, например, Н. Бор относил применимость принци­па дополнительности не только к фи­зическим наукам, он писал: «цельность живых организмов и характеристики людей, обладающих сознанием, а также и человеческих культур представляют черты целостности, отображение кото­рых требует типично дополнительного способа описания» (Бор, 1971, С. 532). Данное высказывание Н. Бора наводит на мысль, что сама реальность – это резуль­тат взаимодействия, взаимопроникнове­ния волновой природы материи и волно­вой природы сознания. Иными словами, изменение природы сознания потенци­ально может существенно изменить ма­териальный мир, пространство и время. Наряду с этим, по свидетельству В. Гей­зенберга, Н. Бор отстаивал приоритет понимания смысла изучаемого явления перед попытками «скорее угадать пра­вильные математические формулы с по­мощью заключений по аналогии, чем вы­вести их» (Гейзенберг, 1987, С. 50).

Природа психических феноменов в рамках фрактально-голографического конструкта

Принимая основные положения К. Ле­вина о взаимосвязанности динамическо­го поля поведения целостной системы «организм-среда», необходимо, на наш взгляд, данное положение рассмотреть в рамках фрактально-голографического конструкта.

Уже с начала 60-х годов ХХ века К. Прибрам (Pribram, 1971, 1981), обра­тил внимание на определенное подобие концептуальных подходов нейрофизио­логии, психологии и голографии и сфор­мулировал голографическую гипотезу. Суть ее в том, что подобными гологра­фическими свойствами при распреде­ленной обработке данных восприятия обладает вся сеть нейронов нашего моз­га. К этим идеям К. Прибрам пришел, опираясь на ранее выдвинутую им мо­дель мозга, в основе которой лежит по­стулат о том, что многие важные аспекты функций мозга основаны на холографи­ческих (от гр. holos – целостный) прин­ципах. В частности, учитывая, что ней­роны имеют древовидные разветвления аксонов, Прибрам пришел к осмысле­нию того, что, когда электрический сиг­нал достигает конца хотя бы одного та­кого разветвления, он не заканчивает свое существование. Электрический сиг­нал продолжает распространяться далее в виде волн, аналогичных наблюдаемым на поверхности воды, постоянно налага­ющихся друг на друга, между контактиру­ющими друг с другом нейронами. Это, не в последнюю очередь, позволило Приб­раму понять, что волны фактически со­здают бесконечный калейдоскопический ряд интерференционных картин, обес­печивая адаптированность мозга к прин­ципу голографии (Pribram, 1971; 1991).

Модель, основанная на голографиче­ских принципах, позволила К. Прибра­му объяснить такие свойства мозга, как огромный объем памяти и ее дистрибу­тивность, способность сенсорных систем к воображению, ряд важных аспектов ассоциативного воспоминания и мно­гие другие (Pribram, 1971; 1981; 1991). Ряд модельных процессов запоминания и восстановления образов, обладающих голографическими свойствами, получи­ли свое воплощение в псевдооптических нейронных сетях (Кузнецов, Шипилина, 2000).

Наряду с этим, рассмотренная выше область Фурье может, как отмечает С. Гроф (Grof, 1985; Grof S., Grof C., 1980), разбиваться на информационные еди­ницы – логоны, действующие по прин­ципу своеобразных «окон», которые ог­раничивают ширину диапазона. Более того, обработка «окон» может иногда осуществляться в холографической обла­сти, отражая этим функции мозга в рас­пределенном виде. В других же случаях обработка «окон» будет осуществлять­ся в пространственно-временной обла­сти, отражая этим локализацию функций мозга. Иными словами, данная особен­ность обработки «окон» выявляет однов­ременность наличия функций мозга в локализованном и распределенном виде.

Следует отметить, что в животном, как и в растительном мире, широко пред­ставлены проявления РФ и ЗП (Богатых, 2012). Проявления чисел Фибоначчи об­наруживается и на субклеточном уров­не в цитоскелете клетки, как у однокле­точных, например, парамеций-туфелек, так и у многоклеточных. В частности, все нейроны мозга имеют свой собст­венный цитоскелет, это указывает на то, что каждый нейрон обладает своеобраз­ной «нервной личной системой». Причем одной из составляющих цитоскелета яв­ляются микротрубочки, представляющие собой белковый полимер, состоящий из субъединиц и носящий название «тубу­лин». Выявлено, что в основе организа­ции микротрубочек млекопитающих за­ложены как раз числовые отношения Фибоначчи. Так, гексагональный узор ми­кротрубочек состоит из 5 правых и 8 ле­вых винтовых структур, в сумме форми­рующих фибоначчиево число 13. Наряду с этим, в часто встречающихся двойных микротрубочках внешний слой содержит уже 21 ряд димеров тубулина, представля­ющих следующее число Фибоначчи. При этом микротрубочки работают в кванто­во-когерентном режиме, не подвергаясь декогеренции за счет неконтролируемо­го взаимодействия с окружением. Однако отсутствие декогеренции на стадии вы­числения характерно для квантовых ком­пьютеров. Именно числовым отношени­ям Фибоначчи отводится ведущая роль в повышении эффективности микротру­бочек как «информационного процес­сора». Представляя собой своеобразные клеточные автоматы, они могут переда­вать и обрабатывать сложные сигналы в виде волн различных состояний элек­трической поляризации молекул тубу­лина (Hameroff, 1987, 1998; Hameroff, Rasmussen, Mansson, 1988). Иными слова­ми, РФ (числовые отношения) как и ЗП, выступают мощным математическим ин­струментарием, как фрактальной геоме­трии, так и голографии (Богатых, 2010).

Как известно, мозг обладает огромной пластичностью. Потенциальная вычисли­тельная возможность мозга является зна­чительно большей, чем это можно ожи­дать, если бы мозг использовал в качестве простейших вычислительных блоков це­лые нейроны. Мозг, его нейронносинап­совая схема не статична, т.е. не обладает ни постоянными синапсами, ни постоянной их интенсивностью. Интенсивность, по крайней мере, некоторых синаптиче­ских связей изменяется время от време­ни порой быстрее, чем за секунду. Кроме того, изменяются и сами связи. Если бы нейронно-синапсовая схема мозга была статична, она бы была эквивалентна схе­ме компьютера (Penrose, 1989). Упрощая, можно сказать, что, согласно гипоте­зе Пенроуза-Хамероффа, мозг работает скорее, как квантовое, чем как классиче­ское вычислительное устройство.

В качестве примера кратко рассмо­трим участие ЗП и РФ в обеспечении ра­боты функциональных систем и приро­ды сознания. Хорошо известно, что ЗП, представляет собой соотношение толь­ко трех величин, проявляющих опре­деленную закономерность, и при этом в конечном своем выражении выступая прообразом чисел (рядов) Фибоначчи. ЗП, содержа две части, порождает третью, являющуюся качественно новой. Оно, в свою очередь, дает результат, выполня­ет функцию, т.е. становится устойчивой функциональной единицей, отражая, на­ряду с этим, и математический аспект. Бо­лее значимо соотношение ЗП выражено у П.К. Анохина. Он пишет: «Когда наш мозг осуществляет самое начало действия, он уже заряжен и на ожидание результата … Чем не существование определенного соотношения между какими-нибудь дву­мя элементами, которое с необходимо­стью определяет величину третьего: то есть мозг уже знает, что есть и ждет то, что надо. А есть соотношение, выраженное либо в вещи, либо как-нибудь абстракт­но. … Еще не реализованное действие уже захватывает мозг, настраивает его на ожи­дание предстоящих результатов и на по­следующую оценку этих результатов, … как совершенно четко очерченную функцию этой системы» (Анохин, 1998, С. 42–43).

Иными словами, данный нервный аппарат, находя в поиске единствен­но нужную реакцию, в конечном ито­ге осуществляет завершение и процесса, и соотношения. ЗП, как и ЧФ, выступая здесь своеобразным инвариантом, может выступать инструментом качественно­го и количественного изучения, напри­мер, функциональных систем в теории функциональных систем (ТФС) П.К. Ано­хина, оправдывая в целом логический пе­реход от изоморфности результата, как системообразующего фактора, к его ма­тематической (информационной) ин­терпретации (Богатых, 2008). Более того, именно ЗП, как и РФ, в своем математиче­ском выражении обеспечивают работаю­щей функциональной системе осущест­вление широчайшего спектра функций организма, отражая при этом количест­венное проявление процесса разверты­вания целостности при выявлении ко­лоссального разнообразия тех или иных композиций. Здесь в более полной мере осуществляется принцип фрактальной, можно сказать, фрактально-голографи­ческой (многомерной) развертки. Данная развертка раскрывает многомерное про­странство объекта, играя при этом, в це­лостном континууме, конкретную роль. А именно, роль меры, указывая этим так­же на то, что весь логический инструмен­тарий поисковых процедур, основанный на методе использования фибоначчие­вой стратегии, как и ЗП, является логикой структурного оптимума, который в наи­большей мере выявляется при анализе немарковских процессов.

Именно микротрубочки, как отмече­но выше, управляют функционировани­ем мозга. Следовательно, в процессах, осуществляющихся в микротрубочках, должно быть что-то отличное от простых вычислений. Гипотеза Хамероффа-Пенро­уза основана на том положении, что та­кая вычислительная активность должна предполагать микроскопическую кван­товую когерентность, объединенную не­ким тонким образом с макроскопическим поведением (Hameroff, 1998; Hameroff, Rasmussen, Mansson,1988). На наш взгляд, данное объединение микроскопической квантовой когерентности с макроскопи­ческим поведением может быть обуслов­лено следующим положением. А именно, сопряженностью числовых соотношений Фибоначчи, заложенных в организации микротрубочек нервных клеток, и рабо­ты функциональных систем организма в рамках стратегии числовых отношений РФ, ЗП, а также соответственно обобщаю­щих золотых S-пропорций и фибоначчи­евых S-инвариантов (Богатых, 2010). Бо­лее того, рассмотренный математический инструментарий фрактальной геометрии (РФ, ЗП) и голографии (самоподобия в представлении символьной информа­ции) (Богатых, 2012) отражает собой су­щественную особенность. ЗП отражает собой иррациональность процессов и яв­лений природы, тогда как РФ – целочи­сленность ее организации, а их совокуп­ность (РФ и ЗП) отражает диалектическое единство их противоположностей: непре­рывного (континуального) и дискретного, так свойственного процессам мышления, чувствования, сознания и, в целом, про­цессам развития психики.

В подтверждение этого, ранее мы рас­смотрели процессуальные закономер­ности фрактальной геометрии – ЗП, РФ, Ѕ-числа Фибоначчи, золотую Ѕ-пропор­цию, фрактальность каналов в приложении к нейрофункциональным и ней­рофизиологическим процессам в ТФС П.К. Анохина (Богатых, 2008, 2012). В частности, показано, что ЗП, как и РФ (соответственно и Ѕ-числа Фибоначчи и золотая Ѕ-пропорция), выступая здесь своеобразным инвариантом, становят­ся инструментом качественного и ко­личественного изучения нейрофунк­циональных систем мозга, обеспечивая работающей функциональной системе осуществление широчайшего спектра функций организма и отражая при этом количественное проявление процесса развертывания целостности при выяв­лении колоссального разнообразия тех или иных композиций. Более того, они оправдывают в целом логический пе­реход от изоморфности результата, как системообразующего фактора, к его ма­тематической (информационной) ин­терпретации (Богатых, 2008). При этом, играя в целостном континууме конкрет­ную роль, а именно, роль меры, указывая этим также на то, что весь логический инструментарий поисковых процедур, основанный на методе использования фибоначчиевой стратегии, как и ЗП, яв­ляется логикой структурного оптимума.

Использование нами математиче­ских и информационных составляющих фрактальной геометрии, таких как золо­тая пропорция и ряды (числа) Фибонач­чи, природа фрактальных аттракторов, а также ряд математических отношений (математические прогрессии, немарков­ские процессы), позволило по-новому взглянуть, как на эволюционный процесс живого, так и на отдельные его проявле­ния (Богатых, 2006, 2007, 2010). Данный математический инструментарий, при­мененный при анализе природы поли­морфических рядов в растительном и животном мире, природы гомологиче­ских рядов наследственной изменчиво­сти Вавилова, теории функциональных систем П.К. Анохина, способствовал фор­мулированию дискретно-непрерывной (дискретно-континуальной) интерпрета­ции эволюции органического мира (Бо­гатых, 2006, 2010).

Разнообразие растительных и живот­ных организмов проявляет себя через ту или иную математическую формулу: а) ряды, образуемые цветками и соцве­тиями, а также законы листорасположе­ния большинства растений и с винто­вым, и со спиральным расположением семян (в головках подсолнечника) или чешуй (в шишках сосновых), формулы которых соответствуют тем или иным РФ; б) раковины многих моллюсков (на­утилоидей, аммоноидей, гастропод и др.), а также фораминифер (одноклеточных животных) соответствуют геометриче­ским классам спиралей (архимедоваой, логарифмической и др.); в) проявление чисел ЗП в строении тел многих живых организмов, включая человека (Богатых, 2012). Важно при этом отметить, что в основе всех этих математических от­ношений (РФ, математических прогрес­сий, как и ЗП) просматривается принцип итерации, отраженный в математической формуле вида Z_n+1= Z²_n+ C.

Голографическая модель Прибрама позволила объяснить многие парадок­сальные свойства мозга, такие как ди­стрибутивность памяти, огромный ее объем, способность сенсорных систем к воображению, многие важные аспек­ты ассоциативного воспоминания, про­екцию образов из области памяти и т.д. В дальнейшем голографический подход способствовал широкому его привлече­нию при объяснении уже феноменов не только мышления и чувствования, но и процесса сознания (Grof, 1985; Grof S., Grof C., 1980; Прибрам, 1975). Следова­тельно, кодирование информации пред­ставляет собой операцию, свойственную не только искусственным системам, но и человеческому мозгу.

Эффективной частью человеческой памяти также является ее способность к перекодированию информации. Иными словами, учитывая, что человек реагирует на те или иные события при взаимодей­ствии с окружающей средой, как на мен­тальном, так и на биологическом уровне, способность нервной системы человека к перекодированию информации при­способлена великолепно (Pribram, 1971, 1981, 1991), и формы перекодирования фактически безграничны. Как следствие, природа восприятия личностью объек­тивного мира (истинной реальности) также безгранична, имея при этом, на первый взгляд, противоречивую особен­ность.

Следует отметить, что использование математической и информационной со­ставляющей фрактально-голографиче­ского конструкта будет в определенной мере отвечать на проблему семантики и грамматики, так как семантический анализ, т.е. анализ системы значений (понятий, конструктов, категориальных структур) может выступать в качестве основного способа описания содержа­ния сознания и механизмов его измене­ния. Так, например, Л.С. Выготский, гово­ря о понятийном мышлении, предлагает закон эквивалентности понятий, распре­деляя их при этом по классам (между ко­торыми существуют определенные свя­зи) в виде своеобразной пирамиды. Он пишет, что «всякое понятие может быть обозначено бесчисленным количеством способов с помощью других понятий» (Выготский, 1982, С. 273). При этом до­бавляет, что это отчасти соответствует своеобразному подобию: «как любое чи­сло может быть получено бесконечным количеством арифметических комби­наций других чисел» (Выготский, 1982, С. 275). Возможно, математические ана­логии в законе эквивалентности понятий будут соответствовать понятию числа в математике, так как математика есть пу­стая форма, способная вместить любое содержание. «Мгновенная мысль может относиться к мысли, сформулированной словами, как алгебраическая формула к ряду чисел, в который она развертыва­ется» (Витгенштейн, 1994, С. 188). Ины­ми словами, знаки, символы, синтаксис, как и грамматика, по-видимому, долж­ны также рассматриваться как составля­ющие итерационных процессов ЗП, РФ, немарковских процессов, обеспечиваю­щих логический инструментарий поис­ковых процедур.

Заключение

Подытоживая, можно отметить, что Фрактал как геометрическая форма обла­дает голографическим свойством. Имен­но голографическое свойство фрактала, а также самоподобие фрактально-голографического конструкта позволяет ос­мысливать его синергетическое при­влечение при объяснении феноменов идеального – процессов мышления, чув­ствования, сознания. Данные процессы человек разворачивает в процессе своей экзистенции самоподобным, фракталь­но-голографическим способом спон­танно в соответствии с особенностями той культуры, в которой он сформиро­вался как человек. Существенную роль здесь играет инструментарий фракталь­ной размерности (фрактальный рост). Он, в частности, представляет собой по­казатель, меру заполнения пространства фрактальной структуры, где фрактальная линия осуществляет выход, своеобразно вторгаясь за пределы одномерного про­странства в двухмерное, а фрактальная плоскость, со своей стороны, частично выходит в трехмерное пространство. Ряд авторов постулируют, что, хотя живые существа и занимают трехмерное про­странство, их организация приближается к четырехмерному пространству (West et. al., 1999). То есть, фрактальные структу­ры, осуществляют добавочное четырех­мерное измерение жизни. По аналогии можно сказать, что сознание человека в процессе познания окружающей дей­ствительности – истинной реальности, «достраивает» евклидову целочисленную размерность фрактальной, дробной раз­мерностью. Этим актом осуществляется заполнение той пустоты, которую так не любит природа. Иными словами, «приро­да не терпит пустоты» (Богатых, 2007).

Следует также отметить, что объе­динение микроскопической кванто­вой когерентности с макроскопическим поведением не в последнюю очередь об­условлено процессами, основанными на принципе обратной связи, когда резуль­тат одной итерации является началь­ным значением следующей итерации, отраженный математической формулой вида Z_n+1= Z²_n+ C. Данной формуле со­ответствует ряд рассмотренных взаимо­сопряженных и взаимосвязанных ма­тематических отношений (принципов и подходов): математические прогрес­сии, немарковские процессы, ЗП, РФ, как и обобщающие золотые S-пропор­ции и фибоначчиевые S-инварианты, последовательность Морса-Туэ, после­довательность Фибоначчи, преобразо­вание Прибрама и т.д. Ряд этих математических соотношений имеет, в рамках природы фрактально-голографического конструкта, свое приложение при ана­лизе биологических (Богатых, 2012), социальных, научно-технических и гу­манитарно-художественных систем (Го­лицын, 1997; Копцик и др., 2004; Петров, 2004). Фрактальная геометрия (опираясь на свои принципы), как и в целом фрак­тально-голографический конструкт, по­зволяет, на наш взгляд, объяснить или, по крайней мере, подступиться к объ­яснению ряда других еще не решенных проблем. В частности, особенностей и парадоксов биологической эволюции и ее механизмов, а также многих проблем и парадоксов осцилляций живого веще­ства, начиная от простейших, например, цианобактерий, до работы мозга живот­ных и человека и анализа развития и ре­ализации интеллектуальных систем в гу­манитарно-художественном и научном творчестве.

Учитывая, что человек при взаимодей­ствии с окружающей средой реагирует на те или иные события, как на ментальном, так и на биологическом уровне, необхо­димо осуществлять следующий прием. Для объяснения привлекать особенность преобразований Фурье, в основе которых любой самый сложный паттерн может быть разложен в ряд регулярных волн. Обратное преобразование, в свою оче­редь, переводит волновой паттерн снова в изображение. Наличие широкого спек­тра перекрывания элементов, входящих в систему при максимально возможных отношениях элементов фрактально-го­лографического конструкта, обуслов­ливает их взаимосодействие, взаимо­проникновение и постоянный переход (перекодировка) идеального (фрактальности при всем ее математическом ап­парате) в материальное образование (физика голограммы). Причем, данный переход осуществляется как в одну, так и в другую сторону, постоянно обогащая и обновляя элементы данных конструктов.

Таким образом, языком кодирования- перекодирования является и дух, и ма­терия. Все это указывает на то, что про­тивоположности здесь своеобразно уравновешиваются в неразличенность, но они при этом по-прежнему потенци­ально существуют. Все это, в определен­ной мере, косвенно отвечает на ряд во­просов, которые пытался разрешить К. Левин в своей теории поля. Будет ли это «парадигма числа», либо «парадигма чи­слового поля» в психологии, или что-то подобное – время покажет.

Возникает вопрос. Не является ли осно­вополагающим в данном функционирова­нии кодирования-перекодирования работа самоподобной сопряженности числовых соотношений Фибоначчи, заложенных в организации микротрубочек нервных кле­ток, и работы функциональных систем организма в рамках стратегии числовых от­ношений РФ, ЗП, а также соответственно обобщающих золотых S-пропорций и фи­боначчиевых S-инвариантов?

И последнее. По меткому выражению Давида Рюэля в эволюционной биологии, как и в других областях знания (экология, психология, социальные науки) матема­тический аппарат, описывающий про­цессы эволюции с условием влияния ха­оса, только начинает прокладывать себе дорогу. В настоящее время влияние хаоса в данных науках находится не столько на уровне количественной науки, сколько на уровне научной философии. Однако, продолжает Давид Рюэль, прогресс возможен и здесь: «… не забывайте, что раз­мышления Пуанкаре о предсказуемости в метеорологии тоже когда-то были лишь научной философией, а теперь эта об­ласть превратилась в количественную на­уку» (Рюэль 2001, С. 78).

Литература:

Азроянц Э.А., Харитонов А.С., Шелепин Л.А. Немарковские процессы как новая парадигма // Вопросы философии. – 1999. – № 7. – С. 94–104.

Анохин П.К. Избранные труды. Кибернетика функциональных систем. – Москва : Медицина, 1998. – 397 с.

Богатых Б.А. Фрактальные структуры живого и эволюционный процесс // Журнал общей биологии. – 2006. – Т. 67. – № 4. – С. 243–255.

Богатых Б.А. Фрактальная природа постнеклассического познания // Философские науки. – 2007. – № 6. – С. 27–40.

Богатых Б.А. Фрактальность и теория функциональных систем // Нелинейный мир. – 2008. – Т. 6. – № 9–. С. 491–499.

Богатых Б.А. Фрактально-голографический конструкт и природа сознания // XIII Всероссийская научно-техническая конференция «Нейроинформатика-2011» : сборник научных трудов. В 3-х ч. Ч. 2. – Москва : НИЯУ МИФИ, 2010. – С. 34–44.

Богатых Б.А. Фрактальная природа живого: системное исследование биологической эволюции и природы сознания. – Москва : ЛИБРОКОМ ; URSS, 2012. – 256 с.

Бор Н. Квантовая физика и философия // Бор Н. Избр. науч. труды. В 2 тт. Т. 2. – Москва, 1971. – С. 526–532.

Бройль де Луи. «Революция в физике» (Новая физика и кванты). – Москва: Атомиздат, 1965. 232 с.

Витгенштейн Л. Философские работы. В 2 ч. Ч. 1. – Москва : Гносис. 1994.

Выготский Л.С. Мышление и речь // Собр. соч. В 6 тт. Т. 2. – Москва : Педагогика, 1982. – С. 5–361.

Гейзенберг В. Шаги за горизонт. – Москва, 1987. – 368 с.

Голицын Г.А. Информация и творчество: на пути к интегральной культуре. – Москва : Русский мир, 1997. – 304 с.

Копцик В.М., Рыжов В.П., Петров В.М. Этюды по теории искусства: диалог естественных и гуманитарных наук. – Москва : ОГИ, 2004. – 368 с.

Кроновер Р.М. Фракталы и хаос в динамических системах. Основы теории. – Москва : Постмаркет, 2000. – 352 с.

Кузнецов О.П., Шипилина Л.Б. Псевдооптические нейронные сети – полная прямолинейная модель и методы расчета ее поведения // Известия АН. Сер. Теория и системы управления. – 2000. – № 5. – С. 168–176.

Левин К. Динамическая психология : избранные труды. – Москва : Смысл, 2001. – 572 с.

Мандельброт Б. Фрактальная геометрия природы. – Москва : Институт компьютерных исследований, 2002. – 656 с.

Налимов В.В. Разбрасываю мысли. В пути и на перепутье. – Москва : Прогресс-Традиция, 2000. – 344 с.

Пенроуз Р. Новый ум короля: о компьютерах, мышлении и законах физики / общ. ред. В.О. Малышенко. – Москва : Эдиториал УРСС. – 2003. – 384 с.

Петров В.М. Количественные методы в искусствознании. – Москва : Академический проект, 2004. – 432 с.

Рюэль Д. Случайность и хаос. – Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. – 192 с.

Современная западная философия : словарь / сост. и отв. ред. В.С. Малахов, В.П. Филатов. – Москва : ТОН – Остожье, 2000. – 554 с.

Шелепин Л.А. Становление новой парадигмы // Философия науки. Вып. 7: Формирование современной естественнонаучной парадигмы. – Москва, 2001. – 270 с.

Шредер М. Фракталы, хаос, степенные законы. – Ижевск : НИЦ «Регулярная и хаотическая динамика», 2005. – 528 с.

Bohm, D.J. (1986) A New Theory of the Relationship of Mind and Matter. Journal of the American Society for Psychical Research, 80(2), 91–123.

Bohm, D., & Hiley, B. (1994) The undivided universe. Routledge, London.

Grof, S. (1985) Beuond the Brain. Albany N.Y., State University of New York Press.

Grof, S., & Grof, C. (1980) Beyond the Death. L.: Thames I Hudson.

Hameroff, S.R. (1987) Ultimate computing. Biomolecular Consciousness and NanoTechnology, Elsevier Science Publishers B.V.

Hameroff, S.R., Rasmussen, S., & Mansson, D. (1988) Molecular automata in microtubules: basic computational logic of the living state? Artificial Life, SFI studies in the sciences of complexity (ed. C. Langton). Addison-Wesley, New York.

Hameroff, S.R. (1998) Quantum computation in brain microtubules? The Penrose–Hameroff “Orch OR” model of consciousness. Philosophical Transactions of the Royal Society. London Series A, 356, 1869–1896.

Levin, K. (1936) Principles of topological Psychology. New York; McGraw Hill, 231.

Mandelbrot, B. B. (1980) Fractal aspects of the iteration of z → λ (1-z) for complex λ, z. Annals NY. Acad. Sciences, 357, 249–259.

Mandelbrot, B. B. (1982) The fractal Geometry of Nature. Freeman, San Francisco.

Penrose, R. (1989) The Emperor’s New Mind. New York: Oxford Univ. Press.

Pribram, K.H. (1971) Languages of the Brain: Experimental paradoxes and principles in neuropsychology. Stanford Univ., Prentice-hall, inc. Englewood cliffs, new jersey.

Pribram, K.H. (1981) Non-Locality and Localization: A Review of the Place of the Holographic Hypothesis of Brain Function in Perception and Memory. Preprint for the Tenth JCUS. November.

Pribram, K.H. (1991) Brain and perception: holonomy and structure in figural processing. Lawrence Erlbaum Assoc, New Jersey.

West, G.B., Brown, J.H., & Enguist, B.J. (1999) The fourth dimension of life: fractal geometry and allometric scaling of organism. Science, 284(5420), 1677–1679. doi: 10.1126/science.284.5420.1677