Стресс-реакция на холод: энтропийная и хаотическая оценка.

Еськов Валерий Матвеевич Сургутский государственный университет Ханты­ Мансийского автономного округа — Югры

Филатов Михаил Александрович Сургутский государственный университет Ханты­ Мансийского автономного округа — Югры

Зинченко Юрий Петрович Федеральный научный центр психологических и междисциплинарных исследований, Московский государственный университет имени М.В. Ломоносова

Стрельцова Татьяна Владимировна Сургутский государственный университет Ханты­ Мансийского автономного округа — Югры

Эффект Н.А. Бернштейна по выяв­лению особенностей организа­ции движений с позиций «повторение без повторений», открыл новую эпоху в изучении сложных систем – complexity. До настоящего времени этот эффект никем так и не был изучен и не­смоделирован. Постуральный тремор сейчас с позиций новой, разрабатыва­емой нами теории хаоса-самооргани­зации (ТХС) реально представляет на­глядный пример организации движений без повторений (Еськов, 2015, 2016а, 2016б; Майстренко, 2009; Русак, 2014; Филатова, 2015). Эта проблема сейчас нами расширена до понимания произ­вольных и непроизвольных движений и роли хаоса в организации любых ви­дов движения (Гавриленко, 2013, 2015; Добрынина, 2015; Дудин, 2011; Еськов, 2013, 2015). Одновременно, такой под­ход может служить связующим звеном при переходе от движения физическо­го к движению абстрактному в фазовом пространстве состояний (ФПС) вектора состояния x = x(t) = (x1, x2, …, xm)T любой биомеханической системы. В настоящее время хаотические биомеханические системы обычно представляют в рам­ках детерминированного хаоса как осо­бый вид движения, которое совершенно некорректно описывать в рамках традиционной статистики, столь широко рас­пространённой в психологии (Адайкин, 2007; Ануфриев, 2008; Гавриленко, 2013; Еськов, 2004).

Попытки построения детерминист­ских и стохастических моделей в изуче­нии биомеханических процессов (в част­ности теппинга или тремора) неизбежно приводят к изучению возможности моделирования хаотической динамики и по­стурального тремора, и теппинга. При этом возникает одна из фундаменталь­ных задач психологии: чем произволь­ное движение отличается от непроизвольного? Ответ на этот вопрос касается и психологов, и физиологов, что сближает позиции этих двух наук. Решение этой проблемы – ключ к пониманию особен­ностей гомеостаза и эволюции любых биосистем – complexity (Еськов, 2004, 2010а, 2010б, 2012, 2013), в нашем случае речь идёт о психологическом гомеоста­зе как сохранении стабильного психиче­ского состояния.

В новом эффекте Еськова-Зинченко численно доказывается почему любой интервал треморограммы (ТМГ) будет уникальным и неповторимым. Это опи­сывается в эффекте Еськова – Зинченко не только для выборок ТМГ, но и их амплитудно-частотных характеристик (АЧХ), автокорреляционных фун­кций A(t) и фрактальных размерностей. Иными словами, ТМГ и ее любой участок будут уникальны и неповторимы, а лю­бой анализ этого участка с позиции стохастического подхода будет применим только для конкретного интервала вре­мени Δt1. В другой момент времени все статистические параметры будут други­ми и, соответственно, мы будем получать другие результаты стохастическо­го анализа как ТМГ, так и других видов движения (на других интервалах време­ни Δt2, Δt3,…, Δtn) (Гавриленко, 2013, 2015; Добрынина, 2015; Дудин, 2011; Еськов, 2013, 2015; Еськов, 2012, 2013, 2015а, 2015б, 2016а, 2016б).

Все статистические характеристики любых движений будут показывать раз­ные статистические функции f(x), раз­ные их АЧХ, A(t), другие характеристики. Тогда возникает базовый вопрос: может ли сознание человека точно управлять процессом движения (или где граница произвольности?) и какова роль ВНД? Ответы на эти вопросы для психологии имеют фундаментальное значение. Это понимал Н.А. Бернштейн, но количест­венное изучение движений «без повто­рений» было сделано только в наше вре­мя (Ануфриев, 2008; Гавриленко, 2013; Еськов, 2016; Филатова, 2015).

1. Оценка статичности тремора в рамках энтропийного подхода

Исследования проводились на базе Сургутского государственного универ­ситета (СурГУ) в период 2014 – 2015 го­дах. Во все три группы входили студен­ты СурГУ (мужского и женского пола), средний возраст 21 год в каждой группе (студенты старших курсов).

Сразу отметим, что при квантовании треморограмм мы получали некоторые выборки координат x1 = x 1(t), которые представляли положение пальца в про­странстве по отношению к датчику регистрации координаты xi (положение пальца в пространстве). Регистрировался набор дискретных величин xi, т.е. выбо­рок треморограмм xi, как непрерывно из­меняющихся координат. Эти выборки xi для каждого интервала Δtj (j = 1, 2, …, n, где n = 15 обычно в наших исследованиях) статистически обрабатывались. Далее x1(t) дифференцировался, т.е. находилась скорость движения конечности x2(t) = dx1/dt и получался вектор x(t) = (x1, x2)T, в таком двумерном фазовом простран­стве. Причём x1 и скорость x2 с пози­ций физики образовывали сопряжённые координаты (Гавриленко, 2013; Еськов, 2016а, 2016б) для некоторого вектора x = x(t) = (x1, x2)T в двумерном фазовом пространстве состояний (ФПС).

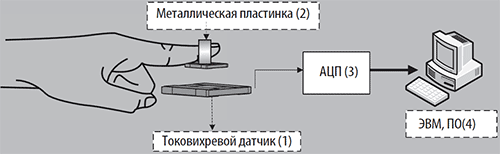
Рис 1. Схема биоизмерительного комплекса регистрации тремора и теппинга

Вся установка включала в себя токо­вихревой датчик (1), усилители сигнала, аналого-цифровой преобразователь – АЦП и ЭВМ, которая кодировала и со­храняла информацию для каждого интервала Δtj в виде отдельных файлов (выборок xi) с реальной длительностью T = 5 сек для каждой треморограммы. Металлическая пластина (2), которая крепилась к пальцу, обеспечивала реги­страцию Δxi с точностью, 0,1 мм в част­ном диапазоне от 0 Гц до 1000 Гц, что весьма затруднительно для акселероме­трических датчиков (или других типов регистраторов).

В целом, мы сейчас говорим о вы­сокоточной регистрации как по х1, так и по частотному диапазону, что позво­ляет оперировать координатой х1 и ско­ростью х2 с высокой точностью (сравнительно с другими работами). Для обработки полученных файлов (вы­борок х1 и х 2 = х 2(t)) первоначаль­но использовались методы статистики (Statistica – 6) для получения статистических функций f(x) (обычно это были непараметрические распределения) а затем определяли АЧХ и A(t). Однов­ременно рассчитывались площади ква­зиаттракторов вектора x(t) = (x1, x2)T, в виде S = Δx1· Δx2, где Δx1 – вариацион­ный размах треморограммы.

Одновременно использовался один из методов стохастики, широко приме­няемой в теории информации и термо­динамике, в виде расчета значения эн­тропии Шеннона. Энтропия Шеннона связана с распределением вероятностей амплитуд колебаний движения. Факти­чески, это мера упорядоченности выбо­рок xi – компонент вектора состояния системы x(t) в фазовом пространстве состояний (ФПС). Характерно, что для странных аттракторов их f(x) для раз­ных Δtj получаются практически оди­наковыми, что для ТМГ невозможно в принципе и это (неповторяемость f(x), АЧХ и A(t)) составляет сейчас основу эф­фекта Еськова-Зинченко (Еськов, 2015; Еськов, 2004, 2010, 2012, 2013, 2015а, 2015б).

Формальное определение энтропии для независимых случайных событий x с n возможными состояниями (от 1 до n, p – функция вероятности) рассчиты­вается по формуле:

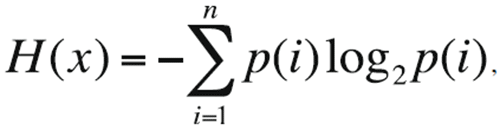
где p – функция вероятности. Для равно­мерного распределения (как мы проверили экспериментально) обычно число k повторов выборок Е бывает k ≈ 98 %, что отлично от ТМГ при расчёте выбо­рок в режиме неизменного психическо­го и физиологического гомеостаза. Отдельно, нами производилось сравнение значений Е с особенностями функцио­нальных состояний испытуемых. Это де­лалось для учёта возможных влияний высшей нервной деятельности (ВНД) на параметры ТМГ (Еськов, 2012, 2013, 2015а, 2015б, 2016а, 2016б).

Главное во всех наших исследова­ниях – это многочисленные повторы измерений у одного и того же челове­ка, находящегося в условиях одинако­вого или разного гомеостаза. При этом можно считать, что психическое состо­яние испытуемого не изменяется во всех 15-ти сериях повторов (по 15-ти вы­борок ТМГ в каждой серии), т.е. мы мо­жем говорить о сохранении одинакового психического гомеостаза (ПГ). Разработка критериев идентификации ПГ и составляет основу наших всех уси­лий, т.е. разработки и применении ТХС в психологии. Итого, в первой части исследования мы имели всего 225 выборок (по 15 серий). Для каждого испытуемого, находящегося в условиях разной адап­тации к холодовым воздействиям (1-я группа без закаливания, 2-я группа – 1 год и 3-я группа – 2 года закалива­ния), в качестве теста было предложено погружение в воду с t = 4 0С. Результа­ты таких испытаний (для одного человека) представлены в табл. 1, где мы де­монстрируем матрицу статистической обработки поведения площади S квази­аттракторов измеряемых треморограмм всех 15-ти серий испытаний до предъявления стресс-агента (охлаждения) (Доб­рынина, 2015; Дудин, 2011; Еськов, 2013, 2015; Еськов, 2004, 2016а, 2016б, Майс­тренко, 2009).

Эти многократные повторы с одной сто­роны выполняли требования «повторений» Н.А. Бернштейна (в его эффекте «повторение без повторений») и позволяли оценить количественно устойчивость параметров ТМГ, оце­нить само понятие психического гомеоста­за – ПГ, насколько этот гомеостаз статичен с позиций традиционной стохастики. В табл. 1 мы представляем результаты расчёта всех 15- ти серий измерений S для квазиаттракторов по 15-ти выборкам в каждой серии. Итого мы имеем 225 разных (!) выборок значений пло­щади квазиаттракторов S для одного и того же испытуемого. Такое многократное повторение опытов с испытуемым, находящимся в одном гомеостазе, раскрывает нам сущность самого психического гомеостаза (ПГ) и особенности поведения квазиаттракторов при одинаковом гомеостазе. Это составляет основу первой ча­сти наших исследований в области устойчиво­сти параметров квазиаттракторов для одного ПГ испытуемого.

№	S1	S2	S3	S4	S5	S6	S7	S8	S9	S10	S11	S12	S13	S14	S15
1	1.57	3	2.46	4.13	1.07	1.94	1.37	2.86	1.74	1.02	1.24	1.05	1.56	0.55	0.14
2	1.33	1.34	2.72	2	2.2	1.99	0.81	3.27	1.9	2.2	1.53	1.31	2.59	1.43	5.78
3	1.7	1.61	1.89	3.99	1.6	0.79	1.49	1.99	1.88	1.86	1.45	1.35	4.83	0.55	9.38
4	1.17	1.36	4.36	2.22	1.64	1.61	1.01	1.46	1.6	2.26	2.86	1.47	2.03	1.03	3.48
5	0.87	1.34	3.06	1.5	3.16	1.04	1.26	4.82	1.3	1.07	1.31	1.91	1.9	1.24	3
6	2.93	1.5	2.82	1.06	4.07	1.08	1.13	6.79	1.69	1.8	1.17	3.84	2.7	1.51	3.8
7	2.08	1.86	5.49	1.25	3.33	5.96	0.51	2.56	0.98	1.62	1.48	1.78	1.6	0.93	2.52
8	0.89	4.2	2	1.32	1.9	3.63	0.98	1.94	1.24	1.1	0.50	1.2	0.97	2.07	4.17
9	0.79	1.74	2.76	1.06	1.1	1.82	0.73	1.49	1.67	1.35	0.83	1.39	0.90	1.42	4.67
10	2.03	1.65	1.42	1.94	0.56	2.15	0.79	2	1.25	2.72	0.46	1.3	1.95	0.49	4.22
11	3.31	2.75	2.88	1.81	2.22	1.46	2.05	3.54	2.82	1.39	0.79	3.15	0.96	2.21	0.90
12	0.97	1.55	1.25	0.85	1.86	0.85	1.02	1.42	1.79	2.02	1.63	2.57	1.29	1.19	6.22
13	1.31	0.73	3.78	1.17	1.54	1.15	1.42	4.01	2.15	1.87	3.18	1.53	1.18	1.02	2.56
14	1.87	1.29	1.94	1.72	2.16	2.36	2.35	1.81	2.07	1.17	0.62	1.38	1.11	3.22	5
15	1.19	0.67	1.9	1.03	0.95	1.96	1.64	2.71	2.07	0.65	0.81	1.41	0.68	2.39	2.4
<S>	1.6	1.77	2.71	1.8	1.96	1.99	1.24	2.84	1.74	1.61	1.33	1.78	1.75	1.42	4.86

Таблица 1. Результаты статистической обработки динамики поведения S*10-6 – площади квазиаттракторов для тремора одного и того же человека для 225 выборок (n = 15 экспериментов по N = 15 выборок в каждом)

Для идентификации существенных или несущественных различий в повторяющих­ся сериях опытов для полученных 225 выбо­рок расчётов также значения энтропии Шен­нона E (разделенных на N = 15 серий по n = 15 выборок ТМГ в каждой) и строилась матри­ца парного сравнения этих всех n выборок энтропий (число серий N = 15) для одного и того же испытуемого. Результаты такого сравнения показали, что число совпадений пар выборок (т.е. возможность их отнесения к одной генеральной совокупности) k=100. Такое же количество числа совпадений получается и для детерминированного хаоса (выборки, по­лученные с помощью стандартного хаотического генератора чисел), т.е. мы имеем почти абсолютную статистическую устойчивость для Е при одном ПГ. Для квазиаттракторов k = 68, что больше 50 % но меньше, чем у Е.

Для хаоса всегда мы получаем одинаковое равномерное распределение (инвариантность мер). Хаотические выборки всегда демонстри­руют 97-99 % совпадений и имеют равномерное распределение, что демонстрирует дина­мический хаос Лоренца-Арнольда. Однако в нашем случае с ТМГ мы с исходными выбор­ками треморограмм этого не имеем. Обычно для ТМГ мы в подобных матрицах имеем чи­сло совпадений не более k ≈ 5 %. В этом заклю­чается эффект Еськова-Зинченко, когда число статистических совпадений выборок ТМГ или теппинграмм невелико и мы имеем хаотиче­скую динамику самих функций распределения f(x). Выборки не могут быть повторяемыми, мы имеем «повторение без повторений» Н.А. Бернштейна. Суммарные значения числа пар совпадений выборок k для всех 15-ти серий представили для тремора устойчивость (стати­стическую) числа совпадений выборок. Общее число совпадений показало среднее значение <k> для всех пятнадцати выборок k в преде­лах <k> ≤ 5 %.

Таким образом, становится очевидным, что энтропия Е даёт почти абсолютную статистическую устойчивость (k_э = 100) а квазиат­тракторы несколько ниже (≈ 70 %), при пси­хическом гомеостазе (в задачах регуляции тремора), а число совпадений выборок самих треморограмм для k при 15-ти сериях опытов тоже даёт высокую степень устойчивости этих k для ТМГ. Однако при этом сами выборки ТМГ очень далеки от стохастики (k ≈ 5 %).

В целом, энтропия Шеннона Е не даёт су­щественных различий для повторов измерения ТМГ подряд от одного испытуемого (100 совпадений пар из 105 разных) в сравнение с повторением самой энтропии. Если система находится в условном статическом состоянии (в гомеостазе регуляции тремора), то выбор­ки повторить два раза подряд (произвольно!) совершенно невозможно, хаотически иногда происходят повторения отдельных выборок. Этот вывод составил основу эффекта Есько­ва-Зинченко в условиях многократных повто­ров испытаний одного человека в одном гоме­остазе (Добрынина, 2015; Дудин, 2011; Еськов, 2013, 2015; Еськов, 2004, 2010а, 2010б, 2012, 2013, 2015а, 2015б, 2016а, 2016б; Майстренко, 2009; Русак, 2014; Филатова, 2015).

2. Локальные охлаждения как стресс – агент: энтропийный подход в оценке треморограмм

Можно ли объективно зарегистрировать изменения психического гомеостаза по пара­метрам ТМГ? Одновременно к этому возника­ет и закономерный второй вопрос – можно ли создать условия, при которых k изменяются, система регуляции тремора перейдёт в другой гомеостаз? В данном параграфе рассматрива­ется влияние локального холодового воздействия на параметры нервно – мышечной си­стемы (НМС) человека (треморограммы) у 3-х групп испытуемых (1-я группа из 15-ти чело­век, не закаливающихся; 2-я группа из 15-ти человек, закаливающихся менее года; 3-я груп­па из 15-ти человек, закаливающихся более 2-х лет). Для каждого испытуемого производилась регистрация параметров ТМГ до и по­сле локального охлаждения кисти, как стресс- воздействия. Очевидно, что охлаждение кисти вызывает определённый психогенный стресс и возмущение психического гомеостаза (на­ряду с физиологическими изменениями в са­мой НМС, т.е. это комплексное воздействие на психику и НМС). Для охлаждения кисть поме­щалась в воду с t = 4 ⁰С (до субъективной поте­ри чувствительности на время τ = 2 мин). При этом охлаждении регистрировались стандар­тно (за τ = 5 сек.) треморограммы и затем для каждой полученной выборки производился расчет энтропии Шеннона Е. В этом случае мы не использовали повтор измерений, а работа­ли с группой в целом (Еськов, 2010, 2012, 2013, 2015а, 2015б).

Отметим, что всегда для тремора у любо­го человека (если нет нарушений двигатель­ных функций) мы имеем небольшие вариации энтропии Е, что доказывает табл. 2. Поэтому использование группы из разных испытуемых или опыты с одним испытуемым дают несуще­ственные различия. Однако, имеет значение психический статус испытуемого или изме­нение его функционального гомеостаза. В на­шем случае мы сейчас имеем сочетанные из­менения и психики (стрессовая ситуация), и физиологических параметров НМС. В целом, очень часто бывает весьма сложно чётко раз­делить доминанты ВНД или специфику физи­ологии периферической НМС, т.к. изменения на периферии всегда вызывают изменения и в ЦНС (ВНД всегда реагирует). Мы считаем, что это приемлемо именно для психофизиологии, которая и должна сочетать учёт психических и физиологических функций человека (Адай­кин, 2007; Ануфриев, 2008; Бернштейн, 1947; Гавриленко, 2013, 2015; Добрынина, 2015; Ду­дин, 2011; Еськов, 2013, 2015).

№	1 группа - Е1		2 группа-Е2		3 группа-Е3
	до	после	до	после	до	после
1	3,86	3,81	3,68	3,67	3,67	3,73
2	3,40	4,05	3,89	3,48	3,83	3,54
3	3,75	3,89	3,86	4,08	3,78	3,59
4	3,75	4,05	3,67	3,81	4,13	3,59
5	3,81	3,97	3,59	3,94	3,57	3,68
6	3,75	3,75	3,92	3,64	3,81	3,54
7	3,60	3,48	4,13	3,56	3,89	3,68
8	4,16	3,78	3,86	3,64	3,64	3,68
9	3,86	3,65	3,81	3,62	3,62	3,83
10	3,89	3,54	3,51	3,67	3,80	3,59
11	3,65	3,84	3,89	4,02	3,88	4,00
12	3,70	3,94	3,75	3,78	3,59	3,54
13	3,94	3,62	3,68	3,35	3,65	3,97
14	3,64	3,75	3,84	3,78	3,86	3,81
15	3,59	3,62	3,78	3,73	3,56	3,67
<Е>	3,76	3,79	3,79	3,72	3,75	3,70
Примечание: Е - значение энтропии Шеннона, <Е> - среднее значение энтропии Шеннона

Таблица 2. Результаты статистической обработки динамики поведения Е – энтропии Шеннона для тремора до и после локального холодового воздействия (до-после) для трех групп испытуемых (1-я группа – 15 человек не закаливающихся, 2-я группа – 15 человек закаливающихся менее года, 3-я группа – 15 человек закаливающихся более 2-х лет)

Как видно из таблицы 2, первая груп­па испытуемых показала динамику (по­сле локального охлаждения конечности) в сторону небольшого увеличения энтро­пии Шеннона (Едо = 3,76, Епосле = 3,79).Од­нако, такие изменения, как показали наши расчёты, статистически не могут быть выявлены. Лица, не занимающиеся закалива­нием организма, образовали эту первую группу, которая, очевидно, имеет и другие физиологические параметры, и психиче­ские (при реакции на стрессорное воздей­ствие – охлаждение кисти). Вторая группа наблюдения представлена людьми более тренированными к холодовому стрессу, использующими закаливающие проце­дуры менее 1 года. Третья группа наблю­дения – закаливающиеся на протяжении длительного времени (более 2-х лет). Оче­видно, что вторая и третья группы показа­ли обратную динамику в сторону уменьшения (хотя и статистически незначимо) значения энтропии: для второй группы (Едо = 3,79, Епосле = 3,72), для третьей груп­пы (Едо = 3,75, Епосле = 3,70).

Это характерные изменения Е в ре­зультате холодового воздействия у лю­дей, которые адаптируются к холоду. Очевидно, что с позиций теоремы Глен­сдорфа-Пригожина мы не получили су­щественных изменений Е, т.е. скорость изменения (прироста) энтропии Р = dE/ dt у нас почти нулевая (с позиций стати­стики). При уходе из положения равно­весия, ВНД, психический гомеостаз не показывают изменение энтропии Е. Со­гласно базовой теоремы термодинамики неравновесных систем, мы в точке рав­новесия (покое) должны иметь Е→max а dE/dt→0. При уходе от равновесия Е должно убывать (у нас для разных групп получается разная динамика Е), а dE/dt должно нарастать (у нас она статистиче­ски не изменяется, т.к. dE/dt = 0). Это характеризует возможности стохастики и ТХС в оценке физиологических эффек­тов тремора при холодовом стрессе, ког­да точно известно об изменении ПГ (воз­никают болевые ощущения).

Из полученных результатов значений энтропии Шеннона, можно видеть, что при выходе организма из стационар­ного состояния (т.е. гомеостаза) изме­нение величин энтропий Е происходит в сотых или в десятых долях значений. Это говорит о слабой чувствительности метода расчета Е при использовании стохастических подходов для измере­ния параметров гомеостаза и сложных биосистем (complexity). Низкая чувст­вительность энтропии Е может не по­казать различий в состоянии системы регуляции тремора при физических воздействиях на испытуемого или эти различия будут статистически недосто­верны (что мы и имеем в табл. 2). Оцен­ка стрессорных холодовых эффектов и изменений в периферическом звене не­рвно-мышечной системы – НМС следу­ет производить другими методами. Мы предлагаем использовать матрицы парных сравнений самих выборок ТМГ или производить расчёт параметров квази­аттракторов (КА) для сравниваемых ТМГ (Еськов, 2010а, 2010б, 2012, 2013, 2015а, 2015б, 2016а, 2016б, Майстренко, 2009; Русак, 2014).

Выводы

1. Психический гомеостаз (как требова­ние неизменности состояния психи­ческих функций человека), о котором впервые начал говорить Н.А. Берн­штейн при изучении организаций движений (Бернштейн, 1947), мож­но оценивать энтропией Шеннона Е в режиме многократных повторений тремора. При этом Е как оказалось, не изменяется существенно, если гомео­стаз не изменяется. Получаемые вы­борки для Е дают почти 95% совпадений их статистических функций f(x). Этого нельзя сказать про сами выбор­ки ТМГ, которые хаотически и непре­рывно изменяются вместе с их (ТМГ) статистическими функциями f(x).

2. Расчет энтропий Шеннона Е может быть использован в оценке адаптив­ных изменений в системе регуля­ции тремора (к холодовым стрессор­ным воздействиям), но он обладает слабой чувствительностью и с пози­ций стохастики может быть вообще не применим для оценки холодового стресса. Требуются другие методы и критерии оценки холодового стресса и других изменений психического го­меостаза.

3. Оценка стрессорных изменений по параметрам треморограмм с помощью энтропии Е не даёт существенных ре­зультатов. Это означает, что теорема Гленсдорфа-Пригожина для биомеха­нических систем не применима, ско­рость изменения энтропии Р=dE/dt=0 при условии, что система регуляции тремора выходит из состояния равно­весия (психического гомеостаза).

Литература:

Адайкин В.А., Еськов В.М., Добрынина И.Ю., Дроздович Е.А., Полухин В.В. Оценка хаотичной динамики параметров вектора состояния организма человека с нарушениями углеводного обмена // Вестник новых медицинских технологий. – 2007. – Т. 14. – № 3. – С. 17-19.

Ануфриев А.С., Еськов В.М., Назин А.Г., Полухин В., Третьяков С.А., Хадарцева К.А. Медико-биологическая трактовка понятия стационарнных режимов биологических динамических систем // Вестник новых медицинских технологий. – 2008. – Т. 15. – № 1. – С. 29-32.

Бернштейн Н.А. О построении движений - М.: Медгиз, 1947. – 254с.

Гавриленко Т.В., Баженова А.Е., Балтикова А.А., Башкатова Ю.В., Майстренко Е.В. Метод многомерных фазовых пространств в оценке хаотической динамики тремора // Вестник новых медицинских технологий. Электронное издание. – 2013. – № 1. – С. 5.

Гавриленко Т.В., Горбунов Д.В., Эльман К.А., Григоренко В.В. Возможности стохастики и теории хаоса в обработке миограмм // Сложность. Разум. Постнеклассика. – 2015. – № 1. – С. 48-53.

Добрынина И.Ю., Горбунов Д.В., Козлова В.В., Синенко Д.В., Филатова Д.Ю. Особенности кардиоинтервалов: хаос и стохастика в описании сложных биосистем // Вестник новых медицинских технологий. – 2015. – Т. 22. – № 2. – С. 19-26.

Дудин Н.С., Русак С.Н., Хадарцев А.А., Хадарцева К.А. Новые подходы в теории устойчивости биосистем – альтернатива теории А.М. Ляпунова // Вестник новых медицинских технологий. – 2011. – Т. 18. – № 3. – С. 336.

Еськов В.В., Вохмина Ю.В., Гавриленко Т.В., Зимин М.И. Модели хаоса в физике и теории хаоса-самоорганизации // Сложность. Разум. Постнеклассика. – 2013. – № 2. – С. 42-56.

Еськов В.В., Гараева Г.Р., Синенко Д.В., Филатова Д.Ю., Третьяков С.А. Кинематические характеристики движения квазиаттракторов в оценке лечебных эффектов кинезотерапии // Вестник новых медицинских технологий. – 2015. – Т. 22. – № 1. – С. 128-136.

Еськов В.М., Еськов В.В., Живогляд Р.Н., Попов Ю.М. Фазатон мозга в норме и при патологии // Вестник новых медицинских технологий. – 2004. – Т. 11. – № 4. – С. 5-8.

Еськов В.М., Еськов В.В., Хадарцев А.А., Филатов М.А., Филатова Д.Ю. Метод системного синтеза на основе расчета межаттракторных расстояний в гипотезе равномерного и неравномерного распределения при изучении эффективности кинезитерапии // Вестник новых медицинских технологий. – 2010а. – Т. 17. – № 3. – С. 106-110.

Еськов В.М., Брагинский М.Я., Козлова В.В., Майстренко Е.В. Диагностика физиологических функций женщин-пловцов Югры методом расчета матриц межкластерных расстояний // Системный анализ и управление в биомедицинских системах. – 2010б. – Т. 9. – № 3. – С. 500-504.

Еськов В.М., Гавриленко Т.В., Дегтярев Д.А., Еськов В.В., Балтикова А.А. Динамика квазиаттракторов параметров непроизвольных микродвижений конечностей человека как реакция на локальные термические воздействия // Вестник новых медицинских технологий. – 2012. – Т. 19. – № 4. – С. 26-29.

Еськов В.М., Добрынина И.Ю., Дрожжин Е.В., Живогляд Р.Н. Разработка и внедрение новых методов теории хаоса и самоорганизации в медицину и здравоохранение // Северный регион: наука, образование, культура. – 2013. – № 1 (27). – С. 150-163

Еськов В.М., Еськов В.В., Филатова О.Е., Филатова Д.Ю. Сравнительная характеристика возрастных изменений сердечно - сосудистой системы населения Севера РФ // Вестник новых медицинских технологий. – 2015а. – Т. 22. – № 3. – С. 15-20.

Еськов В.М., Полухин В.В., Филатова Д.Ю., Эльман К.А., Глазова О.А. Гомеостатические системы не могут описываться стохастически или детерминированным хаосом // Вестник новых медицинских технологий. – 2015б. – Т. 22. – № 4. – С. 28-33.

Еськов В.М., Газя Г.В., Майстренко Е.В., Болтаев А.В. Влияние промышленных электромагнитных полей на параметры сердечнососудистой системы работников нефтегазовой отрасли // Экология и промышленность России. – 2016а. – № 1. – С. 59-63.

Еськов В.М., Еськов В.В., Вохмина Ю.В., Гавриленко Т.В. Эволюция хаотической динамики коллективных мод как способ описания поведения живых систем // Вестн. Моск. ун-та. Сер. 3. Физ. Астрон. – 2016б. – № 2.

Майстренко Е.В., Еськов В.М., Майстренко В.И., Берестовая А.Ф. Сравнительный анализ параметров функциональной асимметрии полушарий и вегетативной нервной системы учащихся // Информатика и системы управления. – 2009. – № 4. – С. 63-65.

Русак С.Н., Молягов Д.И., Бикмухаметова Л.М., Филатова О.Е. Биоинформационные технологии в анализе фазовых портретов погодно- климатических факторов в m-мерном пространстве признаков // Сложность. Разум. Постнеклассика. – 2014. – № 3. – С. 24-28.

Филатова Д.Ю., Вохмина Ю.В., Гараева Г.Р., Синенко Д.В., Третьяков С.А. Неопределенность 1-го рода в восстановительной медицине // Вестник новых медицинских технологий. – 2015. – Т. 22. – № 1. – С. 136-143.